【学习经验】算法板子
说在前面
算法应该是大二上我学的最轻松的一门课了,我有一个完美的开始和一个完美的结束——尽管中间一度每周打算签完到就不做了,非常感谢狗头学长的板子(C++算法板子积累 - Only(AR) 的编程日记),也特别感谢各位助教对我的帮助。下面的板子转pdf打印出来大概有90多页,虽然大部分都用不上,但是!有总比没有好嘛——
Tips
图论 + 重边:最短路记得判断,只存最短的边 + 负环?负边权? + 有重边的情况下判断负环:有负数就存负数,负数越小越好;否则存正数,正数越大越好 + 最短路径 + 单源最短路径:一个点到其他任意点的最短路径 + Bellman-Ford算法:时间\(O(VE)\);可负权重;可回路;可以检测负环,但不能在存在负环的图中计算单源最短路径。 + 有向无环图中的单源最短路径问题:时间\(O(V+E)\);可负权重;不可回路 + Dijkstra算法:时间\(O((V+E)*logV)\);不可负权重;可回路 + 所有结点对的最短路径问题:所有点到所有点的最短路径 + floyd算法:时间\(O(n^3)\)空间\(O(n^2)\);可负权重;可回路;不能检测负环,不能有负环 + 特别地,可以用BFS求无权图最短路径 + 最大流:在一个流网络中,找到从源点到汇点的最大流量。流网络是一个有向图,每条边有一个容量限制,表示通过该边的最大流量。 + Edmonds-Karp算法:时间 \(O(VE^{2})\);适合稀疏图 + Dinic算法:时间 \(O(V^{2}E)\);适合稠密图 + 最大二分匹配:在二分图中找到最大的匹配数。二分图是一种特殊的图,其节点可以分为两个互不相交的集合,使得每条边都连接这两个不同集合中的节点。 + Dinic最小割/最大流算法:时间 \(O(V^2E)\) + 匈牙利算法:时间 \(O(VE)\) + 最小生成树:在连通加权图中,找到一棵包含所有节点的树,使得树中所有边的权重之和最小。目的是找到连接所有顶点的最小总权重的边集。不关心顶点之间的具体路径长度,只关心整体结构的权重最小。 + Prim:时间 朴素版 \(O(V^2)\),堆优化版 \(O(ElogV)\) + Kruskal:时间 \(O(ElogE)\) + 有向无环图 \(G(V,E)\),\(G\) 是半连通的当且仅当有一条路径,这条路径上有图 \(G\) 中所有点:所以判断一个图是不是半连通的只需要判断拓扑序列的相邻节点是否有边
做题思想/技巧 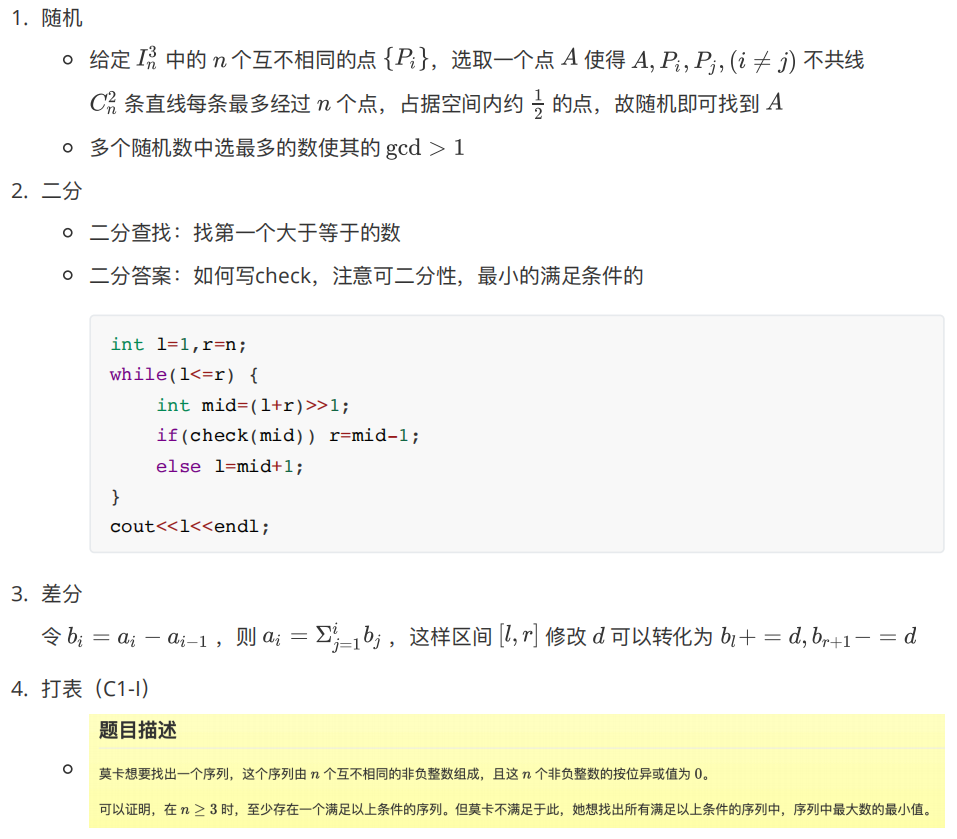
注意事项 + 在对接近 0 的负数四舍五入时应输出
0.00 而非
-0.00:fabs(a) < 0.005 时输出
0.00 + 快速读写 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19//快读
inline ll read(){
ll s=0,w=1;
char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();
return s*w;
}
//快写
inline void out(ll a){
if(a>=10)out(a/10);
putchar(a%10+'0');
}
int main(){
ll n;
n=read();
out(n);
return 0;
}sizeof
,如下方法计算 数组所占空间(KB):
cout << sizeof a/1024 + corner case \(n = 0,1\) \(a_i
= 0, 1e9, -1e9\) 几何中斜率为0 + 初始化 +
多测清空,不要滥用 memset
memset(a, 0, sizeof(int)*(n+1)); 正确
memset(a, 0, sizeof a); 超时 以及 memset
初始化最大值 应为 memset(a, 0x3f, sizeof(int) * (n+1)); +
long long + cin和cout关闭同步流(但关闭后不能用scanf
printf等c语言的输入输出) ios::sync_with_stdio(false) +
cin, cout时用 '' 代替 endl + 数组是否够大 +
浮点数误差:如几何求面积能否直接用整数计算
+ 不要用gets!!!!!!!!!!!!!!!!!! + int max:
2147483647, which is 2^31 - 1 int min: -2147483648,
which is -2^31 long long max: 9223372036854775807,
which is 2^63 - 1 long long min: -9223372036854775808,
which is -2^63 + 一些最大值最小值 用 climits
头文件 INT_MAX INT_MIN LLONG_MAX
LLONG_MIN 1
2
3
4
5
6
7
8
9
10
11#include <iostream>
#include <climits>
int main() {
// 打印整型的最大值和最小值
std::cout << "int 的最大值是:" << INT_MAX << std::endl;
std::cout << "int 的最小值是:" << INT_MIN << std::endl;
// 打印长整型的最大值和最小值
std::cout << "long long 的最大值是:" << LLONG_MAX << std::endl;
std::cout << "long long 的最小值是:" << LLONG_MIN << std::endl;
return 0;
}
cppStart
1 | |
标准库
能按索引访问元素的容器:
vector能遍历的容器:
vector,set,multisetvector(向量): 动态数组;当需要随机访问元素且频繁在末尾添加或删除元素时。queue(队列): FIFO的数据结构;当需要按照添加顺序处理元素时,如广度优先搜索(BFS)。priority_queue(优先队列): 自动排序;当需要处理具有优先级的任务时,如最小生成树算法(Prim’s)或处理事件驱动的系统。stack(栈): LIFO;当需要后进先出的处理顺序时,如深度优先搜索(DFS)、递归算法的辅助数据结构。set(集合): 自动排序,不包含重复元素;当需要存储唯一元素并经常进行查找操作时,如去重、集合运算。multiset(多重集合): 与set类似,但允许存储重复的元素;当需要存储元素并保持有序,但元素可以重复时。
algorithm
1 | |
如 1
2
3
4int a[10] = {5,2,3,4,5};
int b[10] = {5,2,3,4,1};
cout << is_permutation(a, &a[5], b);
is_permutation (c1.begin()+1, c1.end(), c2.begin());
vector
1 | |
queue
1 | |
优先队列的声明
1 | |
结构体的优先队列
重写cmp 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30struct node{
int fir,sec;
void Read() {scanf("%d %d",&fir,&sec);}
}input;
struct cmp1{
bool operator () (const node &x,const node &y) const{
return x.fir<y.fir;
}
};//当一个node x的fir值小于另一个node y的fir值时,x在y后面
struct cmp3{
bool operator () (const node &x,const node &y) const{
return x.fir+x.sec<y.fir+y.sec;
}
};//当一个node x的fri值和sec值的和小于另一个node y的fir值和sec值的和时,x在y后面
priority_queue<node,vector<node>,cmp1> q1;
priority_queue<node,vector<node>,cmp3> q3;
while(!q1.empty()) printf("(%d,%d) ",q1.top().fir,q1.top().sec),q1.pop();
while(!q3.empty()) printf("(%d,%d) ",q3.top().fir,q3.top().sec),q3.pop();
【输入】
1 2
2 1
6 9
9 6
-100 100
-500 20
4000 -3000
【输出】
cmp1: (4000,-3000) (9,6) (6,9) (2,1) (1,2) (-100,100) (-500,20)
cmp3: (4000,-3000) (6,9) (9,6) (1,2) (2,1) (-100,100) (-500,20)
stack
1 | |
set
1 | |
pair
可以用来代替一些便捷的自定义struct。且pair自带小于号,可直接用于排序,第一关键字为第一维升序,第二关键字为第二维升序
1
2
3pair<int,int> p1;
pair<int,string> p2;
pair<double,int> p3;
map
构建⼀个映射关系复杂度为 \(O(logn)\)
1
2
3
4
5map<T1,T2> mp;
map<int,int> mp1;
map<string,int> mp2;
map<int,set<int> mp3;
map<int,vector<int>> mp4;
存图
邻接矩阵
- 存储稠密图
- 实现时需要注意重边与自环。对于最短路问题,可以在重复的边中选择边权最小的一条保留。
- Floyd 算法适合邻接矩阵 ###### 邻接表
1
int d[N][N]; // N 个结点的邻接矩阵 - 存储稠密图
- 对于每个结点,使用一个 vector 保存与之相连的边。 vector实现无权邻接表
- 假设图中总共至多有 N 个结点,每条边不含边权。可以这样实现邻接表:
1
2
3
4
5
6vector<int> g[N]; // N 个结点的邻接表
g[u].emplace_back(v); // 添加一条边 u → v
for (int i = 0; i < g[u].size(); i++) {
int v = g[u][i]; // 遍历 u 的出边 u → v
// · · ·
} - 实际上,可以使用语法糖简化遍历出边的实现,但是并不建议滥用 auto。
1
2
3
4for (auto v : g[u]) {
// 遍历 u 的出边 u → v
// · · ·
}
vector实现有权邻接表 +
对于具有边权或是其他信息的边,可以定义结构体以保存边的信息。
1
2
3
4
5
6struct Edge {
int to; // 边指向的点
int weight; // 边权
}
vector<Edge> g[N]; // N 个结点的邻接表
g[u].emplace_back({v, w}); // 添加边权为 w 的一条边 u → v
pair实现有权邻接表 + 两个元素的有序对
⟨x, y⟩ 可以使用 STL 的 pair 保存。 +
pair ⟨x, y⟩ 之间的大小关系定义为:\(⟨x1, y1⟩ < ⟨x2, y2⟩ ⇐⇒ x1 < x2 ∨ (x1 = x2 ∧
y1 < y2)\) + 第一个元素类型 T1,第二个元素类型 T2 的
pair:pair<T1, T2> p; + 创建一个
pair:p = make_pair(x, y); + 取 pair
的第一个元素:p.first + 取 pair
的第二个元素:p.second + 可以用 pair
实现邻接表。第一个元素保存边指向的点,第二个元素保存边权:
1
2
3
4
5
6
7vector<pair<int, int>> g[N];
g[u].emplace_back(make_pair(v, w));
// 添加边权为 w 的一条边 u → v
for (auto e : g[u]) {
int v = e.first, w = e.second;
// 遍历 u 的出边 u → v,边权为 w
}
char*和string
char* to string
1 | |
string to char*
1 | |
插入排序
1 | |
归并排序 \(O(n log n)\)
1 | |
逆序对计数
1 | |
多数问题
n个数组成一个数组,寻找是否有一个数的数量≥n/2 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50#include <stdio.h>
const int N = 2000000; //定义数组的最大长度
int a[N];
int majorityDC(int a[], int start, int end, int *result) {
// 分治法求解多数问题,*result是数量过半的数的值,数组下标区间为[start, end]
if (start == end) {
*result = a[end];
return 1;
}else{
int m1, m2;
majorityDC(a, start, (start + end) / 2, &m1);
//m1为前半区间[start, (start + end) / 2]的多数
majorityDC(a, (start + end) / 2 + 1, end, &m2);
//m2为后半区间[(start + end) / 2 + 1, end]的多数
int count1 = 0, count2 = 0;
for (int i = start; i <= end; i++) {
if (a[i] == m1) { //count1记录m1在数组a[]中出现的次数
count1++;
}
if (a[i] == m2) { //count2记录m2在数组a[]中出现的次数
count2++;
}
}
if(count1 > ((end - start + 1) / 2)) {
//m1在数组a[]中出现的次数大于数组长度的一半,则m1为多数
*result = m1;
return 1;
}else if(count2 > ((end - start + 1) / 2)) {
//m2在数组a[]中出现的次数大于数组长度的一半,则m2为多数
*result = m2;
return 1;
}else{
return 0; //m1, m2均不是多数,则数组a[]的多数不存在
}
}
}
int main() {
int n, resultDC;
scanf("%d", &n);
for(int i=0; i<n; i++){
scanf("%d\n", &a[i]);
}
if(majorityDC(a, 0, n - 1, &resultDC)){
printf("%d", resultDC);
}else{
printf("Can not find the majority!");
}
return 0;
}
维护堆的性质
- 堆的定义:
- 是一棵完全二叉树
- 每个节点的值都大于或等于其子节点的值,为最大堆;反之为最小堆。
- 堆的存储:一般用数组来表示堆,下标为i的结点的父结点下标为\(\frac{i-1}2\);其左右子结点分别为 \(2i + 1\)、\(2i +
2\)(若数组编号从0开始)。下标为i的结点的父结点下标为\(\frac{i-1}2\);其左右子结点分别为\(2i\)、\(2i +
1\)(若数组编号从1开始) 时间复杂度\(O(lgn)\)或对于树高h的节点来说,时间复杂度\(O(h)\) ###### c递归维护 ###### c非递归维护
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25// 维护最大堆的性质
// arr:一个最大堆的数组
// i:需要调整的堆中的元素
void max_heapify(int arr[], int i, int n){
// 从a[i] a[l] a[r]选择最大的
int l = 2*i+1, r = 2*i+2;
int largest = i;
if(l <= n && arr[l]>arr[largest]){
largest = l;
}
if(r <= n && arr[r]>arr[largest]){
largest = r;
}
// 如果a[i]最大,程序结束
if(largest != i){
swap(&arr[i], &arr[largest]);
max_heapify(arr, largest);
}
}
void swap(int* a, int* b) {
int temp = *b;
*b = *a;
*a = temp;
}##### 建堆 时间复杂度\(O(n)\)1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25// 维护最大堆的性质
// arr:一个最大堆的数组
// i:需要调整的堆中的元素
void max_heapify(int arr[], int start, int end) {
//建立父节点指标和子节点指标
int dad = start;
int son = dad * 2 + 1;
while (son <= end) { //若子节点指标在范围内才做比较
if (son + 1 <= end && arr[son] < arr[son + 1]) //先比较两个子节点大小,选择最大的
son++;
if (arr[dad] > arr[son]) //如果父节点大于子节点代表调整完毕,直接跳出函数
return;
else { //否则交换父子内容再继续子节点和孙节点比较
swap(&arr[dad], &arr[son]);
dad = son;
son = dad * 2 + 1;
}
}
}
void swap(int* a, int* b) {
int temp = *b;
*b = *a;
*a = temp;
}##### 堆排序算法 时间复杂度\(O(nlgn)\) ###### c非递归维护最大堆1
2
3
4
5void build_max_heap(int arr[ ],int n){
int i;
for(i=n/2-1; i>=0; i--) // 建初始堆积
max_heapify(arr, i, n);
}###### c+cpp递归维护最大堆1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41// 堆排序
void heapsort(int arr[], int n){
build_max_heap(arr, n); // 先建堆
for (int i = n - 1; i > 0; i--) {
swap(&arr[0], &arr[i]); // 将第一个元素(剩下的max)和已排好元素前一位做交换
max_heapify(arr, 0, i - 1); // 重新调整
}
}
// 建堆
void build_max_heap(int arr[ ],int n){
int i;
for(i=n/2-1; i>=0; i--) // 建初始堆积
max_heapify(arr, i, n);
}
// 维护最大堆的性质
// arr:一个最大堆的数组
// i:需要调整的堆中的元素
void max_heapify(int arr[], int i, int n){
// 从a[i] a[l] a[r]选择最大的
int l = 2*i+1, r = 2*i+2;
int largest = i;
if(l <= n && arr[l]>arr[i]){
largest = l;
}
if(r <= n && arr[r]>arr[largest]){
largest = r;
}
// 如果a[i]最大,程序结束
if(largest != i){
swap(&arr[i], &arr[largest]);
max_heapify(arr, largest, n);
}
}
void swap(int* a, int* b) {
int temp = *b;
*b = *a;
*a = temp;
}1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39#include <stdio.h>
#include <stdlib.h>
void swap(int* a, int* b) {
int temp = *b;
*b = *a;
*a = temp;
}
// 维护最大堆的性质
// arr:一个最大堆的数组
// i:需要调整的堆中的元素
void max_heapify(int arr[], int start, int end) {
//建立父节点指标和子节点指标
int dad = start;
int son = dad * 2 + 1;
while (son <= end) { //若子节点指标在范围内才做比较
if (son + 1 <= end && arr[son] < arr[son + 1]) //先比较两个子节点大小,选择最大的
son++;
if (arr[dad] > arr[son]) //如果父节点大于子节点代表调整完毕,直接跳出函数
return;
else { //否则交换父子内容再继续子节点和孙节点比较
swap(&arr[dad], &arr[son]);
dad = son;
son = dad * 2 + 1;
}
}
}
// 堆排序算法
void heap_sort(int arr[], int len) {
int i;
//建堆,初始化,i从最后一个父节点开始调整
for (i = len / 2 - 1; i >= 0; i--)
max_heapify(arr, i, len - 1);
//先将第一个元素和已排好元素前一位做交换,再从新调整,直到排序完毕
for (i = len - 1; i > 0; i--) {
swap(&arr[0], &arr[i]);
max_heapify(arr, 0, i - 1);
}
}###### 用cpp的algorithm建堆和堆排序1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35#include <iostream>
#include <algorithm>
using namespace std;
// 维护最大堆的性质
// arr:一个最大堆的数组
// i:需要调整的堆中的元素
void max_heapify(int arr[], int start, int end) {
//建立父节点指标和子节点指标
int dad = start;
int son = dad * 2 + 1;
while (son <= end) { //若子节点指标在范围内才做比较
if (son + 1 <= end && arr[son] < arr[son + 1]) //先比较两个子节点大小,选择最大的
son++;
if (arr[dad] > arr[son]) //如果父节点大于子节点代表调整完毕,直接跳出函数
return;
else { //否则交换父子内容再继续子节点和孙节点比较
swap(arr[dad], arr[son]);
dad = son;
son = dad * 2 + 1;
}
}
}
// 堆排序算法
void heap_sort(int arr[], int len) {
//初始化,i从最后一个父节点开始调整
for (int i = len / 2 - 1; i >= 0; i--)
max_heapify(arr, i, len - 1);
//先将第一个元素和已经排好的元素前一位做交换,再从新调整(刚调整的元素之前的元素),直到排序完毕
for (int i = len - 1; i > 0; i--) {
swap(arr[0], arr[i]);
max_heapify(arr, 0, i - 1);
}
}1
2
3
4
5
6
7
8
9
10
11
12
13
14
15#include <bits/stdc++.h>
using namespace std;
int main() {
vector<int> a = {1,2,3,4,5,6,7,8,9};
make_heap(a.begin(), a.end()); // 造堆
for(int i : a){
cout << i << " ";
}
cout << endl;
sort_heap(a.begin(), a.end()); // 堆排序
for(int i : a){
cout << i << " ";
}
return 0;
}
c优先队列
读最大元素 O(1)
1 | |
移走最大元素 O(lgn)
1 | |
增加某结点的值 O(lgn)
1 | |
插入一个新节点 O(lgn)
1 | |
快速排序
最好情况/平均情况:\(O(nlgn)\)
###### 法1 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47// way1
#include <bits/stdc++.h>
#define keytype int
using namespace std;
void quickSort(keytype k[],int n);
void quick(keytype k[ ],int left,int right);
void swap(int *x, int *y);
void quickSort(keytype k[],int n){
quick(k, 0, n-1);
}
void quick(keytype k[ ],int left,int right){
int i, j;
keytype pivot;
if(left < right){
i = left;
j = right+1;
pivot = k[left];
while(1){
while(k[++i]<pivot && i!=right) { }
while(k[--j]>pivot && j!=left) { }
if(i < j)
swap(&k[i], &k[j]); /*交换K[i]与K[j]的内容*/
else
break;
}
swap(&k[left], &k[j]); /*交换K[s]与K[j]的内容*/
quick(k, left, j-1); /* 对前一部分排序 */
quick(k, j+1, right); /* 对后一部分排序 */
}
}
void swap(keytype *x, keytype *y){
keytype temp;
temp = *x;//取内容交换
*x = *y;
*y = temp;
}
int main() {
int a[100] = {2,3,4,5,1,123,1524,4235,345,34,67,324};
quickSort(a, 12);
for(int i=0; i<12; i++){
printf("%d ", a[i]);
}
return 0;
}1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39// way2 BY K&R
#include <bits/stdc++.h>
#define keytype int
using namespace std;
void quickSort(keytype k[],int n);
void qsort(keytype v[ ],int left, int right);
void swap(keytype v[ ],int i, int j);
void quickSort(keytype k[],int n){
qsort(k, 0, n-1);
}
void qsort(keytype v[ ],int left, int right){
int i, last;
if(left >= right)
return;
swap(v, left, (left+right)/2);// 将中间与left交换,将中间作为基准
last = left; // last: 最后一个比left小的元素
for(i=left+1; i<=right; i++)
if(v[i] < v[left]) // 如果当前元素小于基准元素
swap(v, ++last, i); // last右移,获得新的last
swap(v, left, last); // 把基准元素left放到正确位置
qsort(v, left, last);
qsort(v, last+1, right);
}
void swap(keytype v[ ],int i, int j){
keytype tmp;
tmp = v[i];
v[i] = v[j];
v[j] = tmp;
}
int main() {
int a[100] = {2,3,4,5,1,123,1524,4235,345,34,67,324};
quickSort(a, 12);
for(int i=0; i<12; i++){
printf("%d ", a[i]);
}
return 0;
}
快速排序的随机化版本
最坏情况:\(O(n^2)\)
期望运行时间:\(O(nlgn)\)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40#include <bits/stdc++.h>
#include <random>
using namespace std;
int randomized_partition(int a[], int p, int r);
void randomized_quiksort(int a[], int p, int r);
int partition(int a[], int p, int r);
void randomized_quiksort(int a[], int p, int r){
if(p < r){
int q = randomized_partition(a, p, r); // 随机选择一个元素作为基准,并进行划分
randomized_quiksort(a, p, q-1);
randomized_quiksort(a, q+1, r);
}
}
int randomized_partition(int a[], int p, int r){
int i = rand()%(r-p)+p; // 在[p, r]范围内随机选择一个索引作为基准
swap(a[r], a[i]);
return partition(a, p, r); // 调用partition函数进行划分
}
int partition(int a[], int p, int r){
int x = a[r];
int i = p-1; // i指向小于基准的最后一个元素
for(int j=p; j<=r-1; j++){
if(a[j] <= x){
i++; // i右移
swap(a[i], a[j]); // 交换元素,将小于基准的元素移到左边
}
}
swap(a[i+1], a[r]); // 将基准元素交换到正确的位置
return i+1; // 返回基准元素的最终位置
}
int main() {
int a[100] = {2,3,4,5,1,123,1524,4235,345,34,67,324};
randomized_quiksort(a, 0, 12);
for(int i=0; i<12; i++){
printf("%d ", a[i]);
}
return 0;
}1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28#include <iostream>
#include <algorithm>
#define MAX 1000005
#define ll long long
using namespace std;
int a[MAX];
// 输入:数组array 数组长度n 返回:array的子列中最大的和
ll maxSubArray(int *array, int n) {
ll Max = -0x3f3f3f3f3f3f3f3f;
ll sum = 0;
for (int i = n - 1; i >= 0; i--) {
if (sum < 0) // 如果sum已经<0了,留下sum只会让之后的和更小,所以去掉sum
sum = array[i];
else
sum += array[i];
Max = max(sum, Max);
}
return Max;
}
int main() {
int n;
cin >> n;
for (int i = 0; i < n; i++)
cin >> a[i];
cout << maxSubArray(a, n);
return 0;
}1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43#include <bits/stdc++.h>
using namespace std;
#define MAX 100
#define MIN_VALUE -1
int max(int a, int b){
if(a > b){
return a;
}else{
return b;
}
}
// p为价格表,n为正在切割的钢管长度,r为最大收益
int MEMOIZED_CUT_ROD_AUX(int* p, int n, int* r){
int q;
if(r[n] >= 0){ // 切过这个长度,已经记住了
return r[n];
}
if(n == 0){ // 切一段长度为0的
q = 0;
}else{
q = MIN_VALUE;
for(int i=1; i<=n; i++){ // 左边长度i,右边长度n-i
q = max(q, p[i]+MEMOIZED_CUT_ROD_AUX(p, n-i, r));
}
}
r[n] = q;
return q;
}
// 函数入口 p为价格表 n为正在切割的钢管长度 返回能得到的最大value
int MEMOIZED_CUT_ROD(int* p, int n){
int r[MAX];
for(int i=0; i<=n; i++){
r[i] = MIN_VALUE;// 初始化
}
return MEMOIZED_CUT_ROD_AUX(p, n, r);
}
int main() {
int p[15] = {0, 1, 5, 8, 9, 10, 17,17, 20, 24, 30};
printf("%d", MEMOIZED_CUT_ROD(p, 14));
return 0;
}1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34#include <bits/stdc++.h>
using namespace std;
#define MAX 100
#define MIN_VALUE (-1)
int s[MAX], r[MAX];
void EXTENDED_BOTTOM_UP_CUT_ROD(int *p, int n){
r[0] = 0;
for(int j=1; j<=n; j++){
int q = MIN_VALUE;
for(int i=1; i<=j; i++){
if(q < p[i]+r[j-i]){ // 更好的切割
q = p[i]+r[j-i]; // 更新价格
s[j] = i; // 更新切割方式
}
}
r[j] = q;
}
}
// p:价格表 n:要切的钢条长度
void PRINT_CUT_ROD_SOLUTION(int *p,int n){
EXTENDED_BOTTOM_UP_CUT_ROD(p, n);
// 计算切割下来的每段钢条的长度s[1..n]和最大value r[1..n]
printf("%d\n", r[n]);
while(n > 0){
printf("%d ", s[n]);
n -= s[n];
}
}
int main() {
int p[15] = {0, 1, 5, 8, 9, 10, 17,17, 20, 24, 30};
PRINT_CUT_ROD_SOLUTION(p, 14);
return 0;
}1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50#include <bits/stdc++.h>
using namespace std;
/*
* p: 表示矩阵的规模,矩阵 A_i 的规模用 p_i-1 * p_i 表示
* s: s[i,j]表示A_i A_i+1 ... A_j最优括号化方案的分割点位置k
* m: m[i,j]表示A_i A_i+1 ... A_j所需标量乘法次数的最小值
*/
#define MAX 100
long long p[MAX],m[MAX][MAX],s[MAX][MAX];
void MATRIX_CHAIN_ORDER(int n){
// 初始化
for(int i=1; i<=n; i++){
m[i][i] = 0;
}
for(int l=2; l<=n; l++){ // l is the chain length
for(int i=1; i<=n-l+1; i++){ // 矩阵链的起始位置
int j = i+l-1; // 矩阵链的结束位置
m[i][j] = 9223372036854775807; // long long 最大值
for(int k=i; k<=j-1; k++){ // A_i...A_j 的最优括号化方案的分割点为k
long long q = m[i][k]+m[k+1][j] + p[i-1]*p[k]*p[j];
if(q < m[i][j]){
m[i][j] = q;
s[i][j] = k;
}
}
}
}
}
void PRINT_OPTIMAL_PARENS(long long i, long long j){
if(i == j){
printf("A");
}else{
printf("(");
PRINT_OPTIMAL_PARENS(i, s[i][j]);
PRINT_OPTIMAL_PARENS(s[i][j]+1, j);
printf(")");
}
}
int main() {
int n;
scanf("%d", &n); // n个矩阵
for(int i=0; i<=n; i++){
scanf("%lld", &p[i]);
}
MATRIX_CHAIN_ORDER(n);
printf("%lld\n", m[1][n]); // A_1..A_n所需标量乘法次数的最小值
PRINT_OPTIMAL_PARENS(1,n);
return 0;
}
最长公共子序列
- 子序列:给定一个序列 \(X = <x_1, x_2, ..., x_m>\),另一个序列 \(Z = <z_1,z_2,...,z_k>\) 满足如下条件时成为 \(X\) 的子序列(subsequence),即存在一个严格递增的 \(X\) 的下表序列 \(<i_1,i_2,...,i_k>\),对所有 \(j=1,2,...,k\),满足 \(x_{i_1} = z_j\) 。 例如,\(Z=<B,C,D,B>\) 是 \(X=<A,B,C,B,D,A,B>\) 的子序列,对应的下标序列为 \(<2,3,5,7>\) 。
- 公共子序列:给定两个序列 \(X\) 和 \(Y\) ,如果 Z 既是 X 的子序列,也是 Y 的子序列,我们称它是 X 和 Y 的公共子序列(common subsequence)。
- 最长公共子序列问题(longest-common-subsequence
problem):给定两个序列 \(X =
<x_1,x_2,...,x_m>\) 和 \(Y=<y_1,y_2,..,y_n>\),求 \(X\) 和 \(Y\) 长度最长的公共子序列。 复杂度:\(O(n^2)\)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53#include <stdio.h>
#include <string.h>
#define MAX 100
int c[MAX][MAX];
// 接受字符串x和y,寻找x和y的最长公共子序列
void LCS_LENGTH(char *x, char *y){
// 初始化
int xLen = strlen(x), yLen = strlen(y);
for(int i=1; i<xLen; i++){
if(y[0] == x[i] || c[i-1][0] == 1){
c[i][0] = 1;
}
}
for(int i=1; i<yLen; i++){
if(x[0] == y[i] || c[0][i-1] == 1){
c[0][i] = 1;
}
}
for(int i=1; i<xLen; i++){
for(int j=1; j<yLen; j++){
if(x[i] == y[j]){
c[i][j] = c[i-1][j-1] + 1;
}else if(c[i-1][j] >= c[i][j-1]){ // xi!=yj时f(x)=max(c[i-1,j],c[i,j-1])
c[i][j] = c[i-1][j];
}else{
c[i][j] = c[i][j-1];
}
}
}
}
// 最长公共子序列 输入字符串x,y 字符串长度-1是i,j
void PRINT_LCS(char *x, char *y, int i, int j){
if(i == -1 || j == -1){
return;
}
if(x[i] == y[j]){
PRINT_LCS(x, y, i-1, j-1);
printf("%c ", x[i]);
}else if(c[i-1][j] >= c[i][j-1]){
PRINT_LCS(x, y, i-1, j);
}else{
PRINT_LCS(x, y, i, j-1);
}
}
int main() {
char x[MAX] = "ABCBDAB", y[MAX] = "BDCABA";
LCS_LENGTH(x,y);
PRINT_LCS(x, y, strlen(x)-1, strlen(y)-1);
return 0;
}
最长公共子串
1 | |
最优二叉搜索树
- 最优二叉搜索树问题:给定一个 \(n\) 个不同关键字的已排序的序列 \(K=<k_1,k_2,…,k_n>( k_1<k_2<…<k_n)\) ,我们希望用这些关键字构造一棵二叉搜索树。对每个关键字 \(k\),都有一个概率\(p_i\),表示其搜索频率。有些要搜索的值可能不在 \(K\) 中,因此我们还有 \(n+1个\) 伪关键字 \(d_0,d_1,d_2,...,d+n\) 表示不在 \(K\) 中的值。\(d_0\) 表示所有小于 \(k_1\) 的值,\(d_n\) 表示所有大于 \(k_n\) 的值,对 \(i=1,2,…,n-1\),伪关键字 \(d_i\) 表示所有在 \(k_i\) 和 \(k_{i+1}\) 之间的值。对每个伪关键字 \(d_i\),也都有一个概率 \(q_i\) 表示对应的搜索频率。每个关键字 \(k_i\) 是一个内部结点,而每个伪关键字 \(d_i\) 是一个叶结点。每次搜索要么成功(找到某个关键字 \(k_i\))要么失败(找到某个为关键字 \(d_i\) ),因此有如下公式:\(\sum\limits^{n}_{i=1}p_{i}+\sum\limits^{n}_{i=0}q_{i} = 1\)
- 最优二叉搜索树:对于一个给定的概率集合,我们希望构造一棵期望搜索代价最小的二叉搜索树,我们称之为最优二叉搜索树 复杂度:\(\Theta(n^{3})\)
- 穷举法获得最优二叉搜索树的时间复杂度为 \(\Omega (\frac{4^{n}}{n^{\frac{3}{2}}})\)
##### 最小编辑距离
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99#include <stdio.h>
#define MAX (1000+10)
#define MAXE 1000000000
double p[MAX], q[MAX], w[MAX][MAX], e[MAX][MAX];
// p,q为概率,表示其搜索频率
// e[i,j]为在包含关键字k_i,..,k_j的最优二叉搜索树中进行一次搜索的期望代价
// w[i,j]为在关键字k_i,..,k_j的期望之和
int root[MAX][MAX], n = 5;
void optimalBST(double *p,double *q,int n);
void printRoot();
void printOptimalBST(int i,int j,int r);
int main() {
scanf("%d", &n);
for(int i=1; i<=n; i++){
scanf("%lf", &p[i]);
}
for(int i=0; i<=n; i++){
scanf("%lf", &q[i]);
}
optimalBST(p,q,n);
printf("%lf\n", e[1][n]); // 最小的cost
printRoot(); // 输出所有的根
printf("最优二叉树结构:best structure\n");
printOptimalBST(1,n,-1); // 深度优先遍历输出最优二叉树的结构
return 0;
}
//接受概率列表p和q及规模n作为输入,返回cost表e和根表root。
void optimalBST(double *p,double *q,int n){
// 初始化只包括虚拟键的子树
for (int i = 1;i <= n + 1;++i){
w[i][i - 1] = q[i - 1];
e[i][i - 1] = q[i - 1];
}
// 由上到下,由左到右逐步计算
for (int len = 1;len <= n;++len){
for (int i = 1;i <= n - len + 1;++i){
int j = i + len - 1;
e[i][j] = MAXE;
w[i][j] = w[i][j - 1] + p[j] + q[j]; // i到j的期望之和
// 求取最小代价的子树的根
for (int k = i;k <= j;++k){ // 遍历所有可能的根
// e[i,j] = p_k+(e[i,k-1]+w[i,k-1]) + (e[k+1,j]+w[k+1,j])
// = e[i,k-1]+e[k+1,j] + w[i,j]
double temp = e[i][k - 1] + e[k + 1][j] + w[i][j];
if (temp < e[i][j]){
e[i][j] = temp;
root[i][j] = k;
}
}
}
}
}
// 输出最优二叉查找树所有子树的根
void printRoot(){
printf("各子树的根 roots\n");
for (int i = 1;i <= n;++i){
for (int j = 1;j <= n;++j){
printf("%d ", root[i][j]);
}
puts("");
}
puts("");
}
// 打印最优二叉查找树的结构
// 打印出[i,j]的子树,它是根r的左子树和右子树
void printOptimalBST(int i,int j,int r){
int rootChild = root[i][j];
if (rootChild == root[1][n]){
// 输出整棵树的根
printf("k%d is root\n", rootChild);
printOptimalBST(i,rootChild - 1,rootChild);
printOptimalBST(rootChild + 1,j,rootChild);
return;
}
if (j < i - 1){
return;
}else if (j == i - 1){ // 遇到虚拟键
if (j < r){
printf("d%d is k%d's left son\n", j, r);
}else {
printf("d%d is k%d's right son\n", j, r);
}
return;
}else{ // 遇到内部结点
if (rootChild < r){
printf("k%d is k%d's left son\n", rootChild, r);
}else{
printf("k%d is k%d's right son\n", rootChild, r);
}
}
printOptimalBST(i,rootChild - 1,rootChild);
printOptimalBST(rootChild + 1,j,rootChild);
}1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45#include <iostream>
#include <string>
#define MAX 2005
using namespace std;
int ans;
int dp[2][MAX];
int min3(int a, int b, int c) {
int m = a;
if (b < m)
m = b;
if (c < m)
return c;
return m;
}
int minDistance(string word1, string word2) {
int l1 = word1.length();
int l2 = word2.length();
for (int j = 0; j <= l2; j++)
dp[0][j] = j; // 初始化dp[0]为从空字符串到word2的编辑距离
for (int i = 1; i <= l1; i++) {
// dp[0][j]: word1前i-1个字符转化成word2的前j个字符的编辑距离
// dp[1][j]: word1前i个字符转化成word2的前j个字符的编辑距离
dp[1][0] = i;
for (int j = 1; j <= l2; j++)
if (word1[i - 1] == word2[j - 1])
dp[1][j] = dp[0][j - 1]; // 如果相同,和i-1到j-1的编辑距离一样
else {
dp[1][j] = min3(dp[0][j - 1], dp[0][j], dp[1][j - 1]) + 1;
// dp[0][j-1] 和i-1转成j-1一样,相当于word1换个字
// dp[0][j] 和i-1转成j一样,相当于word1加个字
// dp[1][j-1] 和i转成j-1一样,相当于word1删个字
}
for (int j = 0; j <= l2; j++)
dp[0][j] = dp[1][j];
}
return dp[0][l2];
}
int main() {
string a;
string b;
cin >> a >> b;
cout << minDistance(a, b);
printf("\n%d\n",ans);
return 0;
}1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70// 进行了什么编辑操作
#include <iostream>
#include <string>
#define MAX 2005
using namespace std;
int replace_count = 0;
int delete_count = 0;
int insert_count = 0;
int dp[MAX][MAX] = {};
int min3(int a, int b, int c) {
int m = a;
if (b < m)
m = b;
if (c < m)
return c;
return m;
}
void printOperations(string word1, string word2, int dp[MAX][MAX]) {
int i = word1.length();
int j = word2.length();
while (i > 0 || j > 0) {
if (i > 0 && j > 0 && word1[i - 1] == word2[j - 1]) {
i--;
j--;
} else if (j > 0 && (i == 0 || dp[i][j] == dp[i][j - 1] + 1)) {
insert_count++;
j--;
} else if (i > 0 && (j == 0 || dp[i][j] == dp[i - 1][j] + 1)) {
delete_count++;
i--;
} else {
replace_count++;
i--;
j--;
}
}
}
int minDistance(string word1, string word2) {
int l1 = word1.length();
int l2 = word2.length();
for (int j = 0; j <= l2; j++)
dp[0][j] = j;
for (int i = 1; i <= l1; i++) {
dp[i][0] = i;
for (int j = 1; j <= l2; j++) {
if (word1[i - 1] == word2[j - 1])
dp[i][j] = dp[i - 1][j - 1];
else
dp[i][j] = min3(dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]) + 1;
}
}
printOperations(word1, word2, dp);
return dp[l1][l2];
}
int main() {
string a;
string b;
cin >> a >> b;
int distance = minDistance(a, b);
cout << distance << endl;
printf("Replace: %d\n", replace_count);
printf("Delete: %d\n", delete_count);
printf("Insert: %d\n", insert_count);
return 0;
}
最长单调子序列/LIS(Longest Increasing Subsequence)
\(O(n^2)\) 做法 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23int LIS(){ // a为目标数组 ans为最终得到的最长单调子序列的长度
int ans=1;
for(int i=1; i<=n; i++){//枚举子序列的终点
dp[i]=1;// 初始化为1,长度最短为自身
for(int j=1; j<i; j++){//从头向终点检查每一个元素
if(a[i]>a[j]){
dp[i]=max(dp[i],dp[j]+1); // 状态转移
}
}
ans=max(ans,dp[i]); // 比较每一个dp[i],最大值为答案
}
return ans;
}
int main(){
while(cin>>n){
for(int i=1; i<=n; i++){ // 下标从1开始
cin>>a[i];
}
int ans=LIS();
cout<<ans<<"\n";
}
return 0;
}
\(O(nlgn)\) 做法 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24// 严格单调递增子列的长度
int lsrsa(const vector<int> &a) {
vector<int> sa;
for (auto x: a) {
if (sa.empty() || x > sa.back()) // 如果sa为空或x>sa的最后一个元素
sa.push_back(x);
else
// 如果x<=sa的最后一个元素,二分查找找到sa中第一个>=x的数,并用x替换它。
// 实际上是在尝试找到更小的元素替代sa中的元素,这样后续可能可以添加更多的元素到sa中,从而形成一个更长的子序列。
*lower_bound(sa.begin(), sa.end(), x) = x;
}
return (int) sa.size();
}
// 单调不减子列的长度
int lrsa(const vector<int> &a) {
vector<int> sa;
for (auto x: a) {
if (sa.empty() || x >= sa.back()) // 如果sa为空或x>=sa的最后一个元素
sa.push_back(x);
else // 如果x<sa的最后一个元素,二分查找找到sa中第一个>x的数,并用x替换它。
*upper_bound(sa.begin(), sa.end(), x) = x;
}
return (int) sa.size();
}
活动选择问题
假定有一个 \(n\) 个活动的集合 \(S=\{a_{1}, a_{2},
...,a_{n}\}\),这些活动使用同一个资源,而这个资源在某个时刻只能供一个活动使用,每个活动
\(a_{i}\) 都有一个开始时间 \(s_{i}\) 和一个结束时间 \(f_{i}\) ,其中 \(0\le s_{i}<f_{i}<∞\)
,如果被选中,任务 \(a_i\)
发生在半开时间区间 \([s_i,f_i)\)
期间。如果两个活动时间不重叠,则称他们是兼容的。在活动选择问题中,我们希望选出一个最大兼容活动集。假定活动已按结束时间的单调递增顺序排序。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48#include <bits/stdc++.h>
#define MAX 100
using namespace std;
struct thing{
int startTime, endTime;
};
struct thing things[MAX], ans[MAX]; // ans 参加的活动们
int n;
void Greedy_Activity_Selector(){
printf("0 ");
ans[0] = things[0];
int lastId=0, ansNum = 1; // 当前的最后一个活动的截止时间 当前已经参加的活动数量
for(int i=2; i<=n; i++){
if(things[i].startTime >= things[lastId].endTime){
ans[ansNum] = things[i];
ansNum++;
lastId = i;
printf("%d ", i);
}
}
printf("\n%d", ansNum);
}
int cmp(const void *a, const void *b){
struct thing *pa = (struct thing *)a;
struct thing *pb = (struct thing *)b;
if(pa->endTime < pb->endTime){
return -1;
}else{
if(pa->startTime < pb->startTime){
return -1;
}else{
return 1;
}
}
}
int main() {
scanf("%d", &n);
for(int i=0; i<n; i++){
scanf("%d", &things[i].startTime);
}
for(int i=0; i<n; i++){
scanf("%d", &things[i].endTime);
}
qsort(things, n, sizeof(struct thing), cmp); // 按活动结束时间升序排序
Greedy_Activity_Selector();
return 0;
}
0-1背包
一个正在抢劫商店的小偷发现了 \(n\)
个商品,第 \(i\) 个商品价值 \(v_i\) 美元,重 \(w_i\) 磅,\(v_{i}\) 和 \(w_i\)
都是整数。这个小偷希望拿走价值尽量高的商品,但他的背包最多能容纳 \(W\) 磅重的商品,\(W\) 是一个整数。他应该拿哪些商品呢? ######
二维dp 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20#include<bits/stdc++.h>
using namespace std;
const int N = 1010;
const int MaxW = 10000;
int n, W, v[N], w[N], f[N][MaxW];
int main(){
cin >> n >> W; // n物品数量 W最大重量
for (int i = 1; i <= n; ++i)
cin >> v[i] >> w[i]; // v价值 w重量
for (int i = 1; i <= n; i++){ // 遍历所有物品
for (int j = 0; j <= W; ++j){ // 重量从0到最大重量
f[i][j] = f[i - 1][j]; // 不选择当前物品时的价值,直接继承上一个状态的价值
// 如果当前背包容量可以放下当前物品,则尝试放入,更新最大价值
if (j >= w[i]) f[i][j] = max(f[i][j], f[i - 1][j - w[i]] + v[i]);
}
}
cout << f[n][W] << endl;
return 0;
}1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18#include<bits/stdc++.h>
using namespace std;
const int N = 1010;
int n, W, v[N], w[N], f[N];
int main(){
cin >> n >> W; // n物品数量 W最大重量
for (int i = 1; i <= n; ++i)
cin >> v[i] >> w[i]; // v价值 w重量
for (int i = 1; i <= n; ++i){ // 遍历所有物品
for (int j = W; j >= w[i]; j--){ // 逆序遍历背包容量
// 更新f[j],即考虑放入当前物品i时的最大价值
f[j] = max(f[j], f[j - w[i]] + v[i]);
}
}
cout << f[W] << endl;
return 0;
}1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27#include<bits/stdc++.h>
using namespace std;
#define N 510
long long n, W, v[N], w[N], f[N*N], sumV;
int main(){
memset(f, 0x3f, sizeof(f));
f[0] = 0;
cin >> n >> W; // n个物品 W最大重量
for (int i = 1; i <= n; ++i) {
cin >> w[i] >> v[i]; // w重量 v价值
sumV += v[i]; // 最大价值
}
for (int i = 1; i <= n; ++i){ // 遍历所有物品
for(int j=sumV; j>=v[i]; j--){ // 从最大价值开始,只有在j>=v[i]的情况下才有可能装当前的物品,否则f保持不变
f[j] = min(f[j], f[j-v[i]]+w[i]); // f[j]表示包内物品价值为j时的最小重量
}
}
long long ans = 0;
for(int j=0; j<=sumV; j++){ // 从价值为0到最大价值
if(f[j] <= W){ // 如果包内重量小于W
ans = j; // 更新ans
}
}
cout << ans << endl;
return 0;
}
完全背包
一个正在抢劫商店的小偷发现了 \(n\)
种商品,第 \(i\) 种商品价值 \(v_i\) 美元,重 \(w_i\) 磅,\(v_{i}\) 和 \(w_i\)
都是整数,每种商品都有无限个。这个小偷希望拿走价值尽量高的商品,但他的背包最多能容纳
\(W\) 磅重的商品,\(W\) 是一个整数。他应该拿哪些商品呢?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19#include<bits/stdc++.h>
using namespace std;
const int N = 1010;
int n, W, v[N], w[N], f[N];
int main(){
cin >> n >> W; // 物品种类n 最大容量W
for (int i = 1; i <= n; ++i)
cin >> v[i] >> w[i]; // 价值v 体积w
for (int i = 1; i <= n; ++i){ // 遍历所有物品
for (int j = v[i]; j <= W; j--){ // 顺序遍历背包容量
// 更新f[j],即考虑放入当前物品i时的最大价值
f[j] = max(f[j], f[j - v[i]] + w[i]);
}
}
cout << f[W] << endl;
return 0;
}1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39#include <iostream>
#include <algorithm>
using namespace std;
typedef long long ll;
const int MAX = 1005;
struct {
int cnt;
ll ID[MAX];
} group[MAX]; //用一个结构体来存储每一组的物品编号
ll dp[MAX]; // 最大价值
ll val[MAX]; // 每个物品的价值
ll weight[MAX]; // 每个物品的重量
ll group_bag(int cap, int max_group);
int main() {
int n, W;
cin >> W >> n; // n表示物品数量,W表示背包容量
int a, b, k, max_group = 0;
for (int i = 1; i <= n; i++) {
cin >> a >> b >> k; // a重量 b价值 k物品所在的组号
weight[i] = a;
val[i] = b;
group[k].ID[group[k].cnt++] = i;
max_group = max(max_group, k);
}
cout << group_bag(W, max_group);
return 0;
}
ll group_bag(int W, int max_group) {
for (int i = 0; i <= max_group; i++) // 第一层循环,遍历所有组
for (ll j = W; j >= 0; j--) // 第二层循环,从背包容量W到0倒序遍历
for (int k = 0; k < group[i].cnt; k++) // 第三层循环,遍历当前组内的所有物品
if (j >= weight[group[i].ID[k]]) // 如果当前物品可以放入背包
// 更新dp数组,选择放入或不放入当前物品,取最大值
dp[j] = max(dp[j],dp[j - weight[group[i].ID[k]]] + val[group[i].ID[k]]);
return dp[W];
}1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31//二进制优化
#include<bits/stdc++.h>
using namespace std;
const int MAXN=1e5+10;
int n,W;
int v[MAXN],w[MAXN];
int f[MAXN];
int main(){
cin >> n >> W; // 物品个数n和最大重量W
int cnt = 0; // 记录二进制合成后的物体数
for(int i=1,a,b,s; i<=n; i++) {
cin>> a >> b >> s; // 单个价值a 单个重量b 数量s
int k = 1;
while(k <= s){ // 将每个物品都按照二进制合成
v[++cnt] = k*a;
w[cnt] = k*b;
s -= k;
k *= 2;
}
if(s){
v[++cnt] = s*a;
w[cnt] = s*b;
}
}
for(int i=1; i<=cnt; i++) // 01背包
for(int j=W; j>=v[i]; j--)
f[j] = max(f[j], f[j-v[i]]+w[i]);
cout << f[W];
return 0;
}
分数背包(部分背包)
一个正在抢劫商店的小偷发现了 \(n\)
个商品,第 \(i\) 个商品价值 \(v_i\) 美元,重 \(w_i\) 磅,\(v_{i}\) 和 \(w_i\)
都是整数,对每个商品,小偷可以拿走其一部分,而不是只能做出二元(0-1)选择。。这个小偷希望拿走价值尽量高的商品,但他的背包最多能容纳
\(W\) 磅重的商品,\(W\) 是一个整数。他应该拿哪些商品呢?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50#include <cstdio>
#include <cstdlib>
struct coin{
double w;// 重量
double v;// value
double rou;
};
int cmp(const void *a, const void *b){
struct coin *pa = (struct coin *)a;
struct coin *pb = (struct coin *)b;
if(pa->rou > pb->rou){
return -1;
}else{
return 1;
}
}
int main() {
int n; // 物品个数n
double W; // 最大容量W
scanf("%d%lf", &n, &W);
struct coin gold[110]={};
for(int i=0; i<n; i++){
scanf("%lf%lf", &gold[i].w, &gold[i].v);
gold[i].rou = gold[i].v / gold[i].w;
}
qsort(gold, n, sizeof(struct coin), cmp);
double ans=0;
int now=0;
while(W >= 0){
if(now == n){ // 遍历完所有物品
break;
}
if(gold[now].w < W){ // 放得下整个物品now
W -= gold[now].w;
ans += gold[now].v;
}else{ // 只能放部分
ans += gold[now].v * (W/gold[now].w);
W = 0;
break;
}
now++;
}
printf("%.2lf", ans);
return 0;
}
赫夫曼编码
考虑一种二进制字符编码,其中每个字符用一个唯一的二进制串表示,称为码字。如果使用定长编码,需要用3位来表示6个字符:a=000,b=001,…,f=101。这种方法需要300000个二进制位来编码文件。是否有更好的编码方案呢?
时间复杂度 \(O(nlgn)\)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define MAX 100
// 结构体
typedef struct Node {
char data;
int frequency;
struct Node* left;
struct Node* right;
} Node;
// 创建新节点的函数 return结构体指针类型 data结构体的字符 frequency字符的出现频率
Node* createNode(char data, int frequency) {
Node* node = (Node*)malloc(sizeof(Node));
node->data = data;
node->frequency = frequency;
node->left = NULL;
node->right = NULL;
return node;
}
// Huffman构建函数
Node* buildHuffmanTree(char* inputText) {
int charCount[256] = {};
int length = strlen(inputText);
int i;
// 统计ascii码为inputText[i]的字符的出现次数
for (i = 0; i < length; i++) {
charCount[(int)inputText[i]]++;
}
// 创建叶子结点
Node* nodes[256];
int nodeCount = 0;
for (i = 0; i < 256; i++) {
if (charCount[i] > 0) {
nodes[nodeCount] = createNode((char)i, charCount[i]);
nodeCount++;
}
}
// 依次合并叶子结点
while (nodeCount > 1) {
int minFrequency1 = length + 1; // 当前频率最小的
int minFrequency2 = length + 1; // 当前频率次小的
int index1 = -1;
int index2 = -1;
for (i = 0; i < nodeCount; i++) { // 获得minFrequency1和minFrequency2以及index1 index2
if (nodes[i]->frequency < minFrequency1) {
minFrequency2 = minFrequency1;
index2 = index1;
minFrequency1 = nodes[i]->frequency;
index1 = i;
} else if (nodes[i]->frequency < minFrequency2) {
minFrequency2 = nodes[i]->frequency;
index2 = i;
}
}
// 把最小的和次小的构建为一个树
Node* parent = createNode('\0', nodes[index1]->frequency + nodes[index2]->frequency);
parent->left = nodes[index1];
parent->right = nodes[index2];
// parent放进去,原孩子删掉,最后一个往前移,node数量--
nodes[index2] = parent;
nodes[index1] = nodes[nodeCount - 1];
nodeCount--;
}
return nodes[0];
}
// 编写huffman编码表及打印
void printHuffmanCodes(Node* root, int code[], int top, int codeTable[][256], int codeLengths[]) {
// root根结点 code当前字符的huffman函数 top当前字符的树的深度/huffman编码长度
// codeTable所有字符的huffman编码 codeLengths 所有字符的huffman编码长度
if (root->left) { // 有左子结点
code[top] = 0;
printHuffmanCodes(root->left, code, top + 1, codeTable, codeLengths);
}
if (root->right) { // 有右子节点
code[top] = 1;
printHuffmanCodes(root->right, code, top + 1, codeTable, codeLengths);
}
if (root->left == NULL && root->right == NULL) { // 是叶子节点
codeLengths[(int)root->data] = top; // 字符root->data的编码长度为top
printf("%c:",root->data); // 输出字符root->data
for (int i = 0; i < top; i++) { // 输出字符root->data的编码
codeTable[(int)root->data][i] = code[i];
printf("%d",code[i]);
}
printf("\n");
}
}
// 编码函数
void encodeText(Node* root, char* inputText, char encodedText[], int codeTable[][256], int codeLengths[]){
// 翻译inputText为huffman编码encodedText
int length = strlen(inputText);
int i, j;
for (i = 0; i < length; i++) {
char character = inputText[i]; // 当前处理的字符
int length = codeLengths[(int)character]; // 字符转化成huffman编码后的长度
for (j = 0; j < length; j++) {
encodedText[strlen(encodedText)] = codeTable[(int)character][j] + '0';
}
}
}
// 解码函数
void decodeText(Node* root, char* encodedText, char* decodedText) {
// 翻译huffman编码encodedText为decodedText
int length = strlen(encodedText);
int i = 0;
while (i < length) {
Node* current = root;
while (current->left != NULL || current->right != NULL) {
if (encodedText[i] == '0') {
current = current->left;
} else if (encodedText[i] == '1') {
current = current->right;
}
i++;
}
decodedText[strlen(decodedText)] = current->data;
}
decodedText[strlen(decodedText)] = '\0';
}
int main() {
char inputText[MAX] = "";
gets(inputText);
Node* root = buildHuffmanTree(inputText); // 建树
int code[256]; // 当前字符的huffman编码
int top = 0;
int codeTable[256][256] = {0}; // 所有字符的huffman编码
int codeLengths[256] = {0}; // 所有字符的编码长度
printf("Huffman Codes:\n");
printHuffmanCodes(root, code, top, codeTable, codeLengths);
printf("\n");
printf("InputText:\n%s\n\n",inputText);
// 字符转huffman
char encodedText[1000] = "";
encodeText(root, inputText, encodedText, codeTable, codeLengths);
printf("Encoded Text: \n%s\n\n", encodedText);
// huffman转字符
char decodedText[1000] = "";
decodeText(root, encodedText, decodedText);
printf("Decoded Text: \n%s\n\n", decodedText);
return 0;
}
链式前向星
1 | |
BFS广度优先搜索
邻接矩阵
时间复杂度 \(O(n^2)\)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61#include <bits/stdc++.h>
#define MaxV (10000+10)
using namespace std;
int G[MaxV][MaxV]; // 邻接矩阵
bool visited[MaxV];
int last[MaxV], d[MaxV]; // last[i]点i的前驱结点 d[i]点i的深度
void BFS(int i, int n);
void printPath(int s, int v);
int main(){
int n, m;
scanf("%d%d", &n, &m); // n顶点数 m边数
for(int i=0; i<m; i++){
int u, v;
scanf("%d%d", &u, &v);
G[u][v] = 1;
}
BFS(1, n);
for(int i=2; i<=n; i++){ // 如果是非连通图,该循环保证每个极大连通子图中的顶点都能被遍历到
if(!visited[i])
BFS(i,n);
}
puts("");
printPath(1, 4); // 打印从点1到点4的路径
puts("");
printf("%d", d[4]); // 打印点4的高度
return 0;
}
void BFS(int i, int n){ // i起始顶点 n顶点总数
queue<int> Q; // 待访问的顶点
Q.push(i); // 当前节点
visited[i] = true; // 当前节点被visited过了
printf("v%d->", i);
while(!Q.empty()){
int k = Q.front();
Q.pop();
for(int j=1; j<=n; j++){
if(G[k][j] == 1 && !visited[j]){
Q.push(j); // 当前节点
visited[j] = true; // 当前节点被visited过了
printf("v%d->", j);
d[j] = d[k]+1;
last[j] = k;
}
}
}
}
void printPath(int s, int v){ // s起始顶点 v终点
if(v == s){
printf("%d ", s);
}else if(last[v] == 0){
printf("No path from %d to %d exists", s, v);
}else{
printPath(s, last[v]);
printf("%d ", v);
}
}
邻接表
时间复杂度 \(O(n+e)\)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85#include <bits/stdc++.h>
#define MaxV (10000+10)
using namespace std;
typedef struct edge{ // 定义边结点类型
int adjvex; //指向的点
int weight; //边的权重
struct edge *next; //相邻的边
}ELink;
typedef struct ver{ // 定义顶点结点类型
int vertex; //顶点id
ELink* link; //从此顶点出发的边
}VLink;
VLink G[MaxV];
bool visited[MaxV];
int last[MaxV], d[MaxV]; // last[i]点i的前驱结点 d[i]点i的深度
void BFS(int i, int n);
void printPath(int s, int v);
int main(){
int n, m;
scanf("%d%d", &n, &m); // n顶点数 m边数
for(int i=0; i<m; i++){
int u, v;
scanf("%d%d", &u, &v); // u到v有边,有向的
ELink* e = (ELink*) malloc(sizeof (ELink));
e->adjvex = v, e->weight = 0, e->next = nullptr;
if(G[u].link == nullptr){
G[u].link = e;
}else{
e->next = G[u].link;
G[u].link = e;
}
}
BFS(1, n);
for(int i=2;i<=n;i++){ // 如果是非连通图,该循环保证每个极大连通子图中的顶点都能被遍历到
if(!visited[i])
BFS(i,n);
}
puts("");
printPath(1, 4); // 打印从点1到点4的路径
puts("");
printf("%d", d[4]); // 打印点4的高度
return 0;
}
void BFS(int i, int n){
queue<int> Q; // 待访问的顶点
ELink* p;
Q.push(i); // 当前节点
visited[i] = true; // 当前节点被visited过了
printf("v%d->", i);
while(!Q.empty()){
int k = Q.front();
Q.pop();
p = G[k].link;
while(p != nullptr){ // 如果队列头结点非空
int j = p->adjvex; // 头结点序号
if(!visited[j]){ // 没visited过当前节点
printf("v%d->", j);
visited[j] = true;
Q.push(j);
d[j] = d[k]+1;
last[j] = k;
}
p = p->next; // 下个节点
}
}
}
void printPath(int s, int v){
if(v == s){
printf("%d ", s);
}else if(last[v] == 0){
printf("No path from %d to %d exists", s, v);
}else{
printPath(s, last[v]);
printf("%d ", v);
}
}
DFS深度优先搜索
邻接矩阵
时间复杂度 \(O(n^2)\) 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52#include <bits/stdc++.h>
#define MaxV (10000+10)
using namespace std;
int G[MaxV][MaxV]; // 邻接矩阵
bool visited[MaxV];
int last[MaxV], d[MaxV]; // last[i]点i的前驱结点 d[i]点i的深度
void DFS(int i, int n);
void printPath(int s, int v);
int main(){
int n, m; // n顶点数 m边数
scanf("%d%d", &n, &m);
for(int i=0; i<m; i++){
int u, v;
scanf("%d%d", &u, &v);
G[u][v] = 1;
}
DFS(1, n);
for(int i=2;i<=n;i++){ // 如果是非连通图,该循环保证每个极大连通子图中的顶点都能被遍历到
if(!visited[i])
DFS(i,n);
}
puts("");
printPath(1, 4); // 打印从点1到点4的路径
puts("");
printf("%d", d[4]); // 打印点4的高度
return 0;
}
void DFS(int i, int n){ // i当前结点 n总结点数量
printf("v%d->", i);
visited[i] = true;
for(int j=1; j<=n; j++){
if(G[i][j] == 1 && !visited[j]){
last[j] = i; // 前驱
d[j] = d[i]+1; // 深度
DFS(j, n);
}
}
}
void printPath(int s, int v){ // s起点 v终点
if(v == s){
printf("%d ", s);
}else if(last[v] == 0){
printf("No path from %d to %d exists", s, v);
}else{
printPath(s, last[v]);
printf("%d ", v);
}
}1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74#include <bits/stdc++.h>
#define MaxV (10000+10)
using namespace std;
typedef struct edge{ // 定义边结点类型
int adjvex; //指向的点
int weight; //边的权重
struct edge *next; //相邻的边
}ELink;
typedef struct ver{ // 定义顶点结点类型
int vertex; //顶点id
ELink* link; //从此顶点出发的边
}VLink;
VLink G[MaxV];
bool visited[MaxV];
int last[MaxV], d[MaxV];
void DFS(int i, int n);
void printPath(int s, int v);
int main(){
int n, m;
scanf("%d%d", &n, &m); // n顶点数 m边数
for(int i=0; i<m; i++){
int u, v; // u到v有边,有向的
scanf("%d%d", &u, &v);
ELink* e = (ELink*) malloc(sizeof (ELink));
e->adjvex = v, e->weight = 0, e->next = nullptr;
if(G[u].link == nullptr){
G[u].link = e;
}else{
e->next = G[u].link;
G[u].link = e;
}
}
DFS(1, n);
for(int i=2;i<=n;i++){ // 如果是非连通图,该循环保证每个极大连通子图中的顶点都能被遍历到
if(!visited[i])
DFS(i,n);
}
puts("");
printPath(1, 4); // 打印从点1到点4的路径
puts("");
printf("%d", d[4]); // 打印点4的高度
return 0;
}
void DFS(int i, int n){ // i当前结点 n总结点数量
ELink* p;
printf("v%d->", i);
visited[i] = true;
p = G[i].link;
while(p != NULL){
int j = p->adjvex;
if(!visited[j]){
last[j] = i; // 前驱
d[j] = d[i]+1; // 深度
DFS(j, n);
}
p = p->next;
}
}
void printPath(int s, int v){ // s起点 v终点
if(v == s){
printf("%d ", s);
}else if(last[v] == 0){
printf("No path from %d to %d exists", s, v);
}else{
printPath(s, last[v]);
printf("%d ", v);
}
}
拓扑排序
拓扑排序:对于有向无环图 \(G\) 来说,如果图G包含边 \((u,v)\),则结点 \(u\) 在拓扑排序中处于结点 \(v\) 的前面。 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62#include <bits/stdc++.h>
using namespace std;
#define MAX_VERTICES 10010 // 定义图的最大顶点数
unordered_map<int, vector<int>>graph; // 定义图的结构
struct Edge { //链式前向星,存边的起点、终点、和前驱
int from, to, next;
} e[MAX_VERTICES];
int cnt; //存储的边数
int main() {
int t;
scanf("%d", &t);
while(t--){
int head[MAX_VERTICES] = {}; //下标是起点的表头,存第一个边的编号,初始化为 -1
int id[MAX_VERTICES]={}; //每个点的入度
memset(head, -1, sizeof(head));
graph.clear();
int n, m;
cnt = 1;
scanf("%d%d", &n, &m);
// 读入
for (int i = 1; i <= m; i++) {
int from, to;
scanf("%d%d", &from, &to);
e[cnt].from = from; //起点
e[cnt].to = to; //终点
e[cnt].next = head[from]; //添加
id[to]++;
head[from] = cnt++; //更新表头
graph[from].push_back(to);
}
// 拓扑排序
priority_queue<int> q; // 对于拓扑排序不唯一的情况,先输出序号大的点,再输出序号小的点,即输出字典序最大的拓扑排序
for (int i=1; i<=n; i++) {
if (id[i] == 0)
q.push(i); //把入度为0的点入队
}
vector<int> ans; //数组保存结果
while (!q.empty()) {
int x = q.top(); //出队
q.pop();
ans.push_back(x);
int edge = head[x];
while (edge != -1) {
id[e[edge].to]--; //删除边
if (id[e[edge].to] == 0) //把入度为0的点入队
q.push(e[edge].to);
edge = e[edge].next;
}
}
// 输出形成的拓扑序列
for(int an : ans){
printf("%d ", an);
}
}
return 0;
}
单源最短路径
1 Bellman-Ford算法
- 权重可以为负,可以有回路。时间复杂度\(O(VE)\) ###### 2 有向无环图中的单源最短路径问题 权重可以为负,不能有回路。时间复杂度\(O(V+E)\)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61#include<iostream>
#include<cstdio>
using namespace std;
#define MAX 0x3f3f3f3f
#define N 1010
int nodenum, edgenum, original; //点,边,起点
typedef struct Edge{ //边
int u, v; // 起点 终点
int cost; // 权重
}Edge;
Edge edge[N];
int dis[N], pre[N]; // dis源点到每个顶点的最短距离,pre最短路径的前驱节点
bool Bellman_Ford();
void print_path(int root);
int main(){
scanf("%d%d%d", &nodenum, &edgenum, &original);
pre[original] = original; // 初始化源点的前驱为自己
for(int i = 1; i <= edgenum; ++i){
scanf("%d%d%d", &edge[i].u, &edge[i].v, &edge[i].cost);
}
if(Bellman_Ford())
for(int i = 1; i <= nodenum; ++i){ //每个点最短路
printf("%d\n", dis[i]); // 输出源点到该顶点的最短距离
printf("Path:");
print_path(i); // 打印路径
}
else // 如果存在负权回路,输出提示信息
printf("have negative circle\n");
return 0;
}
bool Bellman_Ford(){
for(int i = 1; i <= nodenum; ++i) //初始化
dis[i] = (i == original ? 0 : MAX);
for(int i = 1; i <= nodenum - 1; ++i) // n-1遍
for(int j = 1; j <= edgenum; ++j)
if(dis[edge[j].v] > dis[edge[j].u] + edge[j].cost){ //松弛
dis[edge[j].v] = dis[edge[j].u] + edge[j].cost;
pre[edge[j].v] = edge[j].u; // 更新前驱节点
}
bool flag = true; // 标记是否存在负权回路 false为有
for(int i = 1; i <= edgenum; ++i)
if(dis[edge[i].v] > dis[edge[i].u] + edge[i].cost){
// 如果还能松弛,则存在负权回路
flag = false;
break;
}
return flag;
}
void print_path(int root){ // 打印最短路的路径(反向)
while(root != pre[root]){ // 前驱
printf("%d-->", root);
root = pre[root];
}
if(root == pre[root])
printf("%d\n", root);
}###### 3 Dijkstra算法1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93#include <bits/stdc++.h>
using namespace std;
#define MAX_VERTICES 10010 // 定义图的最大结点数
#define MAX_EDGE 10010 // 定义图的最大边数
typedef struct edge{ // 定义边结点类型
long long adjvex; //指向的点
long long weight; //边的权重
struct edge *next; //相邻的边
}ELink;
typedef struct ver{ // 定义顶点结点类型
long long vertex, id, d, last;
// 编号 入度 到源点的距离 最短路径中的前驱结点
ELink* link; // 与顶点相连的第一个边结点的指针
}VLink;
// 定义图的结构
VLink G[MAX_VERTICES];
void InitializeSingleSource(long long n, long long s);
void Relax(long long u, long long v, ELink* edge);
int main() {
int t;
scanf("%d", &t);
while(t--){
int n, m, s;
scanf("%d%d%d", &n, &m, &s); // 顶点数 边数 源点
for(int i=0; i<m; i++){
long long u, v, w;
scanf("%lld%lld%lld", &u, &v, &w);
ELink* e = (ELink*) malloc(sizeof (ELink));
e->adjvex = v, e->weight = w, e->next = nullptr;
if(G[u].link == nullptr){
G[u].link = e;
}else{
e->next = G[u].link;
G[u].link = e;
}
G[v].id++;
}
// 拓扑排序
queue<long long > q;
for (int i = 1; i <= n; i++) {
if (G[i].id == 0)
q.push(i); //把入度为0的点入队
}
vector<long long > ans; // 拓扑排序结果
while (!q.empty()) {
long long x = q.front();
q.pop();
ans.push_back(x);
ELink* edge = G[x].link;
while (edge != nullptr) {
G[edge->adjvex].id--;
if (G[edge->adjvex].id == 0) //把入度为0的点入队
q.push(edge->adjvex);
edge = edge->next;
}
}
InitializeSingleSource(n, s); // 初始化
// 松弛结点
for(long long an: ans){
VLink now = G[an];
ELink* temp = now.link;
while (temp != nullptr) {
Relax(an, temp->adjvex, temp);
temp = temp->next;
}
}
// 输出结果
for(long long an: ans){
printf("%lld:%lld ", an, G[an].d);
// 输出每个顶点到源点的最短距离
}
}
return 0;
}
void InitializeSingleSource(long long n, long long s){
for(int i=1; i<=n; i++){
G[i].d = LONG_LONG_MAX;
}
G[s].d = 0;
}
void Relax(long long u, long long v, ELink* edge){
if(G[v].d > G[u].d+edge->weight){
G[v].d = G[u].d+edge->weight; // 更新距离
G[v].last = u; // 更新前驱
}
} - 非负权重的图,可以有回路。时间复杂度\(O((V+E)*logV)\) 标准版
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59#include <iostream>
#include <vector>
#include<queue>
#define MaxV 2005
using namespace std;
struct Edge {
int to;
int weight;
// 构造函数,初始化目标顶点和权重
Edge(int t, int w) :to(t), weight(w) {}
};
//graph用邻接表表示的图 src源节点
vector<int>dijkstra(const vector<vector<Edge>>& graph, int src) {
//储存各个顶点到src顶点的距离
vector<int>dis(MaxV, INT_MAX);
//记录访问过的顶点
vector<bool>vis(MaxV, false);
//用优先级队列来处理距离最短的顶点,pair<int,int>的第一个int存储距离,第二个int存储顶点;
//底层用vector来存储这个队列;greater表示从小到大排
priority_queue<pair<int,int>,vector<pair<int,int> >,greater<pair<int,int> > >pq;
//src顶点到自己的距离为0
dis[src] = 0;
pq.push({0,src});
while (!pq.empty()) {
//v表示当前距离最短的顶点
int v = pq.top().second; pq.pop();
//若是访问过当前顶点则跳过
if (vis[v]) continue;
vis[v] = true;
//访问邻接顶点
for (const auto&edge: graph[v]) {
int t = edge.to;
int w = edge.weight;
if (!vis[t] && w+dis[v]<dis[t]) {
dis[t] = w + dis[v];
pq.push({ dis[t],t });
}
}
}
return dis;
}
int main() {
int n, m, source; // 顶点数 边数 源点
scanf("%d%d%d", &n, &m, &source);
vector<vector<Edge>>graph(MaxV);
for(int i=0; i<m; i++){
int u, v, w;
scanf("%d%d%d", &u, &v, &w);
graph[u].push_back(Edge(v,w)); // 有向图 u到v权重为w
}
vector<int>shortest_path = dijkstra(graph, source); // 起点source
cout << shortest_path[3]; // 顶点source到顶点3的最短路径长度
return 0;
}
所有结点对的最短路径问题
floyd算法
空间复杂度 \(O(V^2)\)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78#include <stdio.h>
#include <limits.h>
#define V 310 // 图中节点的数量
long long dist[V][V], graph[V][V], Path[V][V];
// dist两点间的最短距离 graph图的邻接矩阵 Path最短路径的中转点
void floydWarshall();
void PrintPath(long long u, long long v);
int main() {
int n, m; // 顶点数 边数
scanf("%d%d", &n, &m);
for(int i=0; i<m; i++){
long long u, v, w; // 起点、终点和权重
scanf("%lld%lld%lld", &u, &v, &w);
if((graph[u][v]!=0 && w<graph[u][v]) || graph[u][v] == 0){
// 考虑到可能有重复边
graph[u][v] = w;
}
}
floydWarshall();
int q; // q次询问
scanf("%d", &q);
while(q--){
int u, v;
scanf("%d%d", &u, &v); // 询问的起点和终点
if(u == v){ // u和v是同一个点,距离为0
printf("%d->%d: 0\n", u, v);
}else if(dist[u][v] == LONG_LONG_MAX){ // u不可达v,输出-1
printf("%d->%d: -1\n", u, v);
}else{ // u可达v
printf("%d->%d: %lld\n", u, v, dist[u][v]); // 最短距离
PrintPath(u, v); // 打印最短路径
}
}
return 0;
}
void floydWarshall() {
// 初始化最短路径矩阵
for (int i = 0; i < V; i++)
for (int j = 0; j < V; j++){
if(graph[i][j] != 0){
dist[i][j] = graph[i][j];
}else{
dist[i][j] = LONG_LONG_MAX;
}
if(dist[i][j] < LONG_LONG_MAX && i != j){
Path[i][j] = j; // 初始化路径为直接连接
}else{
Path[i][j] = -1;
}
}
// 更新最短路径矩阵
for (int k = 0; k < V; k++) { // 遍历所有节点作为中转点
for (int i = 0; i < V; i++) { // 遍历所有起点
for (int j = 0; j < V; j++) { // 遍历所有终点
if (dist[i][k] != LONG_LONG_MAX && dist[k][j] != LONG_LONG_MAX && dist[i][k] + dist[k][j] < dist[i][j]) {
// 如果通过k点可以使i到j的距离更短,松弛
dist[i][j] = dist[i][k] + dist[k][j];
Path[i][j] = k; // 更新路径的中转点为k
}
}
}
}
}
// 打印最短路径
void PrintPath(long long u, long long v){
printf("%lld ", u); // 打印起点
while(Path[u][v] != v){ // 当中转点不是终点时
printf("%lld ", Path[u][v]); // 打印中转点
u = Path[u][v]; // 更新起点为中转点
}
printf("%lld\n", v); // 打印终点
}
有向图的传递闭包
- 传递闭包:\(G*=(V,E*)\) ,其中 \(E*=\{(i,j)|如果图G中包含一条从结点i到结点j的路径\}\)
- 用于解决问题:给定有向图,判断对于所有结点对i和j,图G是否包含一条从结点i到结点j的路径
时间复杂度:\(O(n^3)\)
法1:floyd算法每条边权重赋1 法2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43#include <cstdio>
#define V 310 // 图中节点的数量
long long dist[V][V]; // dist[i][j] i到j的可达性
void floydWarshall();
int main() {
int n, m;
scanf("%d%d", &n, &m);
for(int i=0; i<m; i++){
long long u, v, w;
scanf("%lld%lld%lld", &u, &v, &w);
dist[u][v] = 1;
}
floydWarshall();
int q; // q次询问
scanf("%d", &q);
while(q--){
int u, v;
scanf("%d%d", &u, &v);
if(dist[u][v]){ // u可达v,输出1
printf("%d->%d: 1\n", u, v);
}else{ // u不可达v,输出0
printf("%d->%d: 0\n", u, v);
}
}
return 0;
}
void floydWarshall() {
// 初始化最短路径矩阵
for (int i = 0; i < V; i++)
dist[i][i] = 1;
// 更新最短路径矩阵
for (int k = 0; k < V; k++) { // 遍历所有节点作为中转点
for (int i = 0; i < V; i++) { // 遍历所有起点
for (int j = 0; j < V; j++) { // 遍历所有终点
dist[i][j] = dist[i][j] | (dist[i][k] & dist[k][j]);
}
}
}
}
经过固定点的最短路径
 ##### 最大流 ######
Edmonds-Karp算法 时间复杂度 \(O(VE^{2})\),其中 \(V\) 为点的总数,\(E\) 为边的总数
##### 最大流 ######
Edmonds-Karp算法 时间复杂度 \(O(VE^{2})\),其中 \(V\) 为点的总数,\(E\) 为边的总数 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73#include <bits/stdc++.h>
using namespace std;
const int N=210;// 最大节点数量
const int INF=0x7FFFFFFF;
int n,m; // n为节点数,m为汇点编号
int map0[N][N]; // 残留图,表示每条有向边的容量
int pi[N]; //BFS的前驱图
int flow_in[N]; //流入i的最大流量是flow_in[i]
int start,end0; // 源点和汇点
queue<int> q;
int bfs();
int Edmonds_Karp();
int main(){
int i,u,v,cost;
while(scanf("%d%d",&n,&m)!=EOF){ // 读取节点数和汇点编号
memset(map0,0,sizeof(map0));
for(i=0;i<n;i++){
scanf("%d%d%d",&u,&v,&cost);
map0[u][v]+=cost; // 更新残留图的容量
}
start=1,end0=m; // 1是源点,m是汇点
printf("%d\n",Edmonds_Karp());
}
return 0;
}
int bfs(){
int i,t;
while(!q.empty()) q.pop();
memset(pi,-1,sizeof(pi));
pi[start]=0; // 源点的前驱为自己
flow_in[start]=INF;
q.push(start);
while(!q.empty()){
t=q.front();
q.pop();
if(t==end0) break; // 已经走到汇点,循环结束
for(i=1;i<=m;i++){
if(pi[i]==-1 && map0[t][i]){ // 节点i未被访问且t到i有边
flow_in[i] = min(flow_in[t], map0[t][i]); // 更新流入i的最大流量
q.push(i);
pi[i]=t; // i的前驱结点为t
}
}
}
if(pi[end0]==-1) return -1; // 如果汇点未被访问,说明没有增广路径
else return flow_in[m]; // 返回增广路径的流量
}
int Edmonds_Karp(){
int max_flow_in=0; // 流f的流值|f|
int cf_p; // 增广路径的残留容量Cf(p)
while((cf_p=bfs())!=-1){ // 当还有增广路径时
//1. 流值|f|增加本次增广路径的残留容量cf_p
max_flow_in+=cf_p;
//2. 更新残留图
int now=end0;
while(now!=start){
int pre=pi[now]; // 获取前驱节点
map0[pre][now]-=cf_p; //更新正向边的实际容量
map0[now][pre]+=cf_p; //添加反向边
now=pre; // 移动到前驱节点
}
}
return max_flow_in; // 返回最大流
}1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98#include <algorithm>
#include <cstring>
#include <iostream>
#include <queue>
using namespace std;
typedef long long ll;
const int V_MAX = 205; // 最大顶点数
const int E_MAX = 5005; // 最大边数
const ll LL_INF = 0x3f3f3f3f3f3f3f3f;
ll max_stream = 0; // 最大流
int cnt_E = 0;
int n, m, s, t;
struct Edge {
int to; // 边的目标顶点
int nxt; // 下一条边的索引
ll val; // 边的容量
} e[E_MAX * 2]; // 边数组,每条边对应一条正向边和一条反向边
int head[V_MAX]; // 邻接表的头指针数组
int depth[V_MAX]; // 每个顶点的层次
void addEdge(int x, int y, int w);
void read();
bool bfs();
ll Dinic();
int main() {
int T;
cin >> T;
while(T--){
cin >> n >> m >> s >> t; // 顶点数 边数 源点 汇点
cnt_E = 0, max_stream = 0; // 初始化边计数器和最大流
fill(head + 1, head + 1 + n, -1);
read();
cout << Dinic() << '\n';
}
return 0;
}
void addEdge(int x, int y, int w) {
e[cnt_E].to = y;
e[cnt_E].val = w;
e[cnt_E].nxt = head[x];
head[x] = cnt_E++;
}
void read() {
int u, v, w;
for (int i = 0; i < m; i++) {
cin >> u >> v >> w;
addEdge(u, v, w); // 添加正向边
addEdge(v, u, 0); // 添加反向边,容量为0
}
}
bool bfs() { // bfs用于获得层次(分层图)
memset(depth, 0, sizeof(depth));
depth[s] = 1; // 源点的层次为1
queue<int> q;
q.push(s); // 将源点加入队列
while (!q.empty()) {
int u = q.front();
q.pop();
for (int i = head[u]; i > -1; i = e[i].nxt) {
int v = e[i].to;
if (e[i].val && !depth[v]) { // 边有剩余容量且目标顶点未访问
depth[v] = depth[u] + 1; // 更新目标顶点的层次
q.push(v); // 将目标顶点加入队列
}
}
}
if (depth[t] != 0) // 如果汇点可达
return true; // 返回true表示存在增广路径
return false;
}
ll dfs(int pos, ll in) { // DFS用于寻找增广路径并计算流量
if (pos == t) // 如果当前顶点是汇点,则返回当前流量
return in;
ll out = 0; // 初始化当前顶点的流出量为0
for (int u = head[pos]; u > -1 && in; u = e[u].nxt) {
int v = e[u].to;
// 如果边有剩余容量且目标顶点的层次恰好是当前顶点层次加1
if (e[u].val && depth[v] == depth[pos] + 1) {
// 递归调用dfs寻找增广路径,并计算可以流过当前边的流量
ll res = dfs(v, min(e[u].val, in));
e[u].val -= res; // 更新正向边的容量
e[u ^ 1].val += res; // 更新反向边的容量
in -= res; // 减少当前流量
out += res; // 增加流出量
}
}
if (out == 0)
// 如果当前顶点没有流出量,则将其层次设为0,表示在后续的BFS中不会再访问
depth[pos] = 0;
return out;
}
ll Dinic() {
while (bfs()) // 存在增广路径
max_stream += dfs(s, LL_INF);
return max_stream;
}
最大二分匹配
Dinic最小割/最大流算法
时间复杂度 \(O(VE)\) 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92// 最大流等于最小割
#include<iostream>
#include<algorithm>
#include<cstring>
#include<queue>
using namespace std;
const int N = 1e3+10, M = 5e5+1e4+10, INT = 0x3f3f3f3f;
// 最大节点数(至少n+m+2) 最大边数(至少最大边数+n+m,因为有源点汇点的边) 无穷大常量
int e[M], ne[M], f[M], h[N], idx;
// e边的终点 ne下一条边的索引 f边的容量 h每个节点边的起始索引 idx边的索引
int cur[N], d[N]; // cur当前弧优化 d节点层次
// 弧优化通过记录每次DFS搜索的断点,使得下一次DFS可以直接从上次搜索的断点继续,从而跳过那些已经饱和的边
int n, m, eNum, S, T; // n: 节点数, m: 边数, S: 源点, T: 汇点
void add(int a, int b, int c);
int dinic();
bool bfs();
int dfs(int u, int lim);
int main(){
scanf("%d%d%d", &n, &m, &eNum);
S = 0, T = n + m + 1; // 设置源点和汇点
memset(h, -1, sizeof h);
for (int i = 1; i <= n; i++) add(S, i, 1); // 添加源点到左侧点的边
for (int i = n + 1; i <= n+m; i++) add(i, T, 1); // 添加右侧点到汇点的边
for(int i = 1; i <= eNum; i++){
int a, b;
scanf("%d%d", &a, &b);
add(a, b+n, 1); // 起点 终点 容量为1
}
cout << dinic() << "\n"; // 输出二分图最大匹配的边数
for(int i=0;i<idx;i+=2) // 输出二分图匹配的点对
{
if(e[i]>n && e[i]<=n+m && !f[i]) // 是右侧的边且剩余容量为0(这条边在最大流中已经被完全使用)
{
printf("%d %d\n",e[i^1],e[i]-n); // 左侧的点 右侧的点
}
}
return 0;
}
void add(int a, int b, int c){ // a: 起点, b: 终点, c: 容量
e[idx] = b, f[idx] = c, ne[idx] = h[a], h[a] = idx++; // 添加正向边
e[idx] = a, f[idx] = 0, ne[idx] = h[b], h[b] = idx++; // 添加反向边,容量为0
}
// Dinic算法主函数
int dinic(){
int r = 0, flow; // 初始化最大流为0
while(bfs()) // 当BFS可以构建分层图时
while(flow = dfs(S, INT))
r += flow; // 通过DFS寻找增广路径并累加流量
return r; // 返回最大流
}
// BFS用于分层图构建
bool bfs(){
queue<int> q;
q.push(S); // 将源点加入队列
memset(d, -1, sizeof d);
d[S] = 0, cur[S] = h[S]; // 源点的层次为0,初始化当前弧
while(q.size()){
int t = q.front(); q.pop();
for(int i = h[t]; ~i; i = ne[i]){ // 遍历所有邻接边
int ver = e[i]; // 邻接边的终点
if(d[ver] == -1 && f[i]){ // 如果终点未访问且正向边有容量
d[ver] = d[t] + 1; // 更新终点层次
cur[ver] = h[ver]; // 初始化当前弧
if(ver == T) return true; // 如果到达汇点,返回true
q.push(ver); // 将终点加入队列
}
}
}
return false; // 如果无法到达汇点,返回false
}
// DFS用于寻找增广路径
int dfs(int u, int lim){
if(u == T) return lim; // 如果到达汇点,返回剩余流量
int flow = 0; // 初始化当前节点的流量为0
for(int i = cur[u]; ~i && flow < lim; i = ne[i]){ // 遍历当前节点所有邻接边
int ver = e[i]; // 邻接边的终点
cur[u] = i; // 更新当前弧
if(d[ver] == d[u] + 1 && f[i]){ // 如果终点层次正确且正向边有容量
int t = dfs(ver, min(f[i], lim - flow)); // 递归寻找增广路径
if(!t)
d[ver] = -1; // 如果无法增广,更新终点层次为-1
f[i] -= t, f[i^1] += t, flow += t; // 更新正向边和反向边的容量,累加流量
}
}
return flow; // 返回当前节点的流量
}1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42#include<bits/stdc++.h>
using namespace std;
const int N=555; // 定义最大可能的节点数
vector<int> G[N]; // 邻接表,用于存储每个男生的认识的女生的列表
int match[N],vis[N];
// match用于存储谁(i)和谁(match[i])匹配
// vis用于存储当前这一边搜索是否已经让某个男生找过增广路了
bool used[N][N]; // 用于标记某个男生和女生之间是否有边
bool hungary(int p,int op);
int main(){
int n,m,e,a,b; // n男生数 m女生数 e边数 a男生编号 b女生编号
scanf("%d%d%d",&n,&m,&e);
while(e--){
scanf("%d%d",&a,&b); //a范围1~n b范围1~m
if(used[a][b]) //判重边
continue;
used[a][b]=true;
G[a].push_back(b);
}
int ans=0;
for(int i=1;i<=n;i++)
if(hungary(i,i)) // 第i个男生,同时也是第i次搜寻
ans++;
printf("%d\n",ans);
return 0;
}
bool hungary(int p,int op){ // p表示第几个男生,op表示第几趟匹配
if(vis[p]==op) // 如果当前男生在当前轮次已经找过增广路径,返回false
return false;
vis[p]=op;
for(int i:G[p]){ // 对于每个男生p,遍历一遍他认识的女生
if(!match[i]||hungary(match[i],op)){
// 如果当前的女生没被匹配到,自然可以直接让她与当前的男生p进行匹配
// 如果已经被匹配过,则尝试让匹配她的那个男生去再找找看其他女生(开始套娃),
// 如果返回true也可以正常匹配
match[i]=p;
return true;
}
}
return false;
}
最小生成树
prim-朴素版
1 | |
prim-堆优化
1 | |
kruskal
1 | |
傅里叶变换
最高次数为n,次数界可以为n, n+1, n+2, 2n 对于次数界为n的多项式 \(A(x) = \sum\limits_{j=0}^{n-1}a_{j}x^{j}\)
,dft求的是 \(y_{k} =
A(\omega_{n}^{k})=\sum\limits_{j=0}^{n-1}a_{j}\omega_{n}^{kj}\)
即 \(y = DFT_{n}(a)\) 其中 \(ω=cos\frac{2π}{2^{n}}+i\
sin\frac{2π}{2^{n}}\) ###### 多项式乘法-普通版 时间复杂度 \(\Theta(nlgn)\) 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89#include <iostream>
#include <vector>
#include <cmath>
const double Pi = acos(-1);
const int MAX = 4000005; // 字符串最大长度
using namespace std;
typedef long long ll;
struct Complex {
double x, y; // 实部和虚部
Complex operator+(const Complex &b) const {
return {x + b.x, y + b.y};
}
Complex operator-(const Complex &b) const {
return {x - b.x, y - b.y};
}
Complex operator*(const Complex &b) const {
return {x * b.x - y * b.y, x * b.y + y * b.x};
}
} f[MAX], p[MAX], sav[MAX];
void dft(Complex *f, int len);
void idft(Complex *f, int len);
int main() {
int n, m;
cin >> n >> m; // 第一个多项式最多n次,第二个最多m次
for (int i = 0; i <= n; i++)
cin >> f[i].x; // 读入第一个多项式的系数
for (int i = 0; i <= m; i++)
cin >> p[i].x; // 读入第二个多项式的系数
for (m += n, n = 1; n <= m; n <<= 1); // 相乘最多n+m位
dft(f, n); // 对第一个多项式进行DFT
dft(p, n); // 对第二个多项式进行DFT
for (int i = 0; i < n; i++)
f[i] = f[i] * p[i]; // 点乘得到乘积的DFT
idft(f, n); // 对结果进行逆DFT
for (int i = 0; i <= m; i++)
cout << (int) (f[i].x / n + 0.49) << " "; // 四舍五入
return 0;
}
void dft(Complex *f, int len) {
if (len == 1)
return;
Complex *fl = f, *fr = f + len / 2; // 分治法,将数组分为两部分
for (int k = 0; k < len; k++)
sav[k] = f[k]; // 备份原数组
for (int k = 0; k < len / 2; k++) {
fl[k] = sav[k << 1]; // 分配偶数次的系数到左子数组
fr[k] = sav[k << 1 | 1]; // 分配奇数次的系数到右子数组
}
dft(fl, len / 2);
dft(fr, len / 2);
Complex tG = {cos(2 * Pi / len), sin(2 * Pi / len)}; // omega_n单位根
Complex buf = {1, 0}; // omega初始化旋转因子
for (int k = 0; k < len / 2; k++) {
sav[k] = fl[k] + buf * fr[k]; // 合并结果
sav[k + len / 2] = fl[k] - buf * fr[k];
buf = buf * tG; // omega = omega*omega_n更新旋转因子
}
for (int k = 0; k < len; k++)
f[k] = sav[k];
}
void idft(Complex *f, int len) {
if (len == 1)
return;
Complex *fl = f, *fr = f + len / 2;
for (int k = 0; k < len; k++)
sav[k] = f[k];
for (int k = 0; k < len / 2; k++) {
fl[k] = sav[k << 1];
fr[k] = sav[k << 1 | 1];
}
idft(fl, len / 2);
idft(fr, len / 2);
Complex tG = {cos(2 * Pi / len), -sin(2 * Pi / len)}; // 与dft唯一的区别
Complex buf = {1, 0};
for (int k = 0; k < len / 2; k++) {
sav[k] = fl[k] + buf * fr[k];
sav[k + len / 2] = fl[k] - buf * fr[k];
buf = buf * tG;
}
for (int k = 0; k < len; k++)
f[k] = sav[k];
}
多项式乘法-高效版/位逆序版
1 | |
1 | |
高精度乘法
1 | |
最大公约数:欧几里得算法
1 | |
欧几里得算法的扩展形式
1 | |
同余方程 \(ax ≡ b (mod\ m)\)
\(ax ≡ b (mod\ m)\) 即 \(ax - b = km\) 1.
通解形式:线性同余方程 ax ≡ b (mod m)
的通解可以表示为 x = x0 + km/d,其中 x0
是一个特解,k 是任意整数,d = gcd(a, m)。 2.
遍历所有解:解的周期性为
d,我们可以通过遍历 k 从 0 到
d-1 来找到所有可能的解。 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17// 计算同余方程的所有解
int f(long long a,long long b,long long m){
extendedEuclid(a,m);
if(b%d) // 同余方程有解的前提是b是d(a和m的最大公约数的倍数)
return -1;//无解
x=x*(b/d)%m; // 一个特解
for(int i=1; i<=d; i++){ // 遍历所有解的可能
long long tempAns = (x+(i-1)*m/d)%m;
while(tempAns<0){ // 确保解为正数
tempAns += m;
}
if(tempAns < ans){ // 更新解为最小的解
ans = tempAns;
}
}
printf("%lld", ans);
}
字符串匹配
Rabin-Karp算法 双哈希
预处理时间 \(\Theta(m)\),最坏运行时间 \(\Theta((n-m+1)m)\),期望运行时间 \(O(n)+O(m(v+\frac{n}{q}))\)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62#include<iostream>
#include<string>
using namespace std;
void Rabin_Karp_search(const string &T, const string &P, int d, int q1, int q2);
int main() {
string T = "Rabin–Karp string search algorithm: Rabin-Karp"; // 文本字符串
string P = "Rabin"; // 模式字符串
int q1 = 101; // 第一个质数,用于取模运算
int q2 = 103; // 第二个质数,用于取模运算
int d = 52; // a到z 大小写
Rabin_Karp_search(T, P, d, q1, q2);
return 0;
}
// T文本字符串 P模式字符串 字符集的大小 两个用于取模运算的质数
void Rabin_Karp_search(const string &T, const string &P, int d, int q1, int q2){
int m = P.length(); // 模式字符串的长度
int n = T.length(); // 文本字符串的长度
int i, j;
int p1 = 0, p2 = 0; // 模式字符串的双哈希值
int t1 = 0, t2 = 0; // 文本字符串的双哈希值
int h1 = 1, h2 = 1; // 用于计算哈希值的基数
// h的值将是"d的(m-1)次方对q取模"
for (i = 0; i < m-1; i++){
h1 = (h1*d)%q1;
h2 = (h2*d)%q2;
}
// 计算模式字符串和文本字符串第一个窗口的总哈希值
for (i = 0; i < m; i++) {
p1 = (d*p1 + P[i])%q1;
p2 = (d*p2 + P[i])%q2;
t1 = (d*t1 + T[i])%q1;
t2 = (d*t2 + T[i])%q2;
}
// 逐个将模式字符串在文本字符串上滑动
for (i = 0; i <= n - m; i++) {
// 检查当前窗口的文本字符串和模式字符串的双哈希值
// 如果双哈希值匹配,则逐个字符检查
if ( p1 == t1 && p2 == t2 ) {
/* 逐个字符检查 */ for (j = 0; j < m; j++)
if (T[i+j] != P[j])
break;
if (j == m) // 如果哈希值匹配且字符也完全匹配
cout<<"Pattern found at index :"<<i<<"\n";
}
// 为下一个窗口的文本字符串计算哈希值:移除首位数字,添加末位数字
if ( i < n-m ){
t1 = (d*(t1 - T[i]*h1) + T[i+m])%q1;
t2 = (d*(t2 - T[i]*h2) + T[i+m])%q2;
// 如果t为负值,则将其转换为正值
if(t1 < 0)
t1 = (t1 + q1);
if(t2 < 0)
t2 = (t2 + q2);
}
}
}
字符匹配有限自动机
1 | |
KMP算法
时间复杂度 \(O(m+n)\)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43#include <iostream>
#include <vector>
#include <string>
using namespace std;
vector<int> prefix(string str);
int main(){
string text;
string key;
cin >> text; // 文本字符串
cin >> key; // 模式字符串
int kl = key.length();
vector<int> kmp = prefix(key); // 计算模式字符串的KMP前缀表即π
int k = 0;
for(int i = 0; i < text.length(); i++){
// 当匹配长度大于0且当前字符不匹配时,回退到前缀表的相应位置
while (k && key[k] != text[i])
k = kmp[k - 1];
// 如果当前字符匹配,增加匹配长度
if(text[i] == key[k])
k++;
// 如果匹配长度等于模式字符串的长度,输出匹配的位置
if(k == kl)
cout << i - k + 2 << "\n";
}
for(auto x: kmp) // 输出KMP前缀表即π的每个值
cout << x << " ";
return 0;
}
vector<int> prefix(string str){
int l = (int) str.length();
vector<int> pre(l); // 创建一个长度为l的向量来存储前缀表
for(int i = 1; i < l; i++){
int j = pre[i - 1]; // i-1的最大的前缀==后缀
// 如果 j>0(防止死循环) 且当前字符与前缀的最后一个字符不匹配时,回退j的值
while (j && str[j] != str[i])
j = pre[j - 1]; // ababaababab
if(str[j] == str[i]) // 如果当前字符与前缀的最后一个字符匹配,增加j的值
j++;
pre[i] = j; // 设置当前字符的前缀表值
}
return pre;
}
确定连续线段是向左转还是向右转
已知 \(\overrightarrow{p_{0}p_{1}},
\overrightarrow{p_{1}p_{2}}\) 。计算 \((p_{2}-p_{0})\times(p_{1}-p_{0}) =
(x_{2}-x_{0})(y_{1}-y_{0})-(y_{2}-y_{0})(x_{1}-x_{0})\) + 结果
\(<0\) ,则在 \(p_{1}\) 左转 + 结果 \(>0\) ,则在 \(p_{1}\) 右转 + 结果 \(=0\) ,则在 \(p_{0}, p_{1}, p_{2}\) 三者共线
1
2
3
4
5
6
7
8
9
10struct dot{
int x, y;
};
int direction(dot pi, dot pj, dot pk){
// 计算向量pi-pj和向量pk-pj的叉积,用于判断方向
// 如果<0,则pipj pjpk在pj左转
// 如果>0,则pipj pjpk在pj右转
// 否则三者共线
return ((pk.x-pi.x)*(pj.y-pi.y)-(pk.y-pi.y)*(pj.x-pi.x));
}1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36struct dot{
int x, y;
};
// 计算向量pi-pj和向量pk-pj的叉积,用于判断方向
int direction(dot pi, dot pj, dot pk){
return ((pk.x-pi.x)*(pj.y-pi.y)-(pk.y-pi.y)*(pj.x-pi.x));
}
bool onSegment(dot pi, dot pj, dot pk){ // 判断点pk是否在线段pi-pj上
if(min(pi.x, pj.x) <= pk.x && max(pi.x, pj.x) >= pk.x &&
// 判断pk的x坐标是否在pi和pj的x坐标之间
min(pi.y, pj.y) <= pk.y && max(pi.y, pj.y) >= pk.y){
// 判断pk的y坐标是否在pi和pj的y坐标之间
return true;
}
return false;
}
//线段p1p2与p3p4是否相交
bool segmentsIntersect(dot p1, dot p2, dot p3, dot p4){
int d1 = direction(p3, p4, p1);
int d2 = direction(p3, p4, p2);
int d3 = direction(p1, p2, p3);
int d4 = direction(p1, p2, p4);
if(((d1>0 && d2<0)||(d1<0 && d2>0)) && ((d3>0 && d4<0)||(d3<0 && d4>0))){
return true; // 如果两线段在彼此的两侧,则相交
}else if(d1 == 0 && onSegment(p3, p4, p1)){
return true; // 如果p1在p3p4上
}else if(d2 == 0 && onSegment(p3, p4, p2)){
return true; // 如果p2在p3p4上
}else if(d3 == 0 && onSegment(p1, p2, p3)){
return true; // 如果p3在p1p2上
}else if(d4 == 0 && onSegment(p1, p2, p4)){
return true; // 如果p4在p1p2上
}else{
return false;
}
}
确定任意一对线段是否相交
\(O(n^2)\) 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
struct Point {
int x, y;
Point operator+(const Point &b) const {
return {x + b.x, y + b.y};
}
Point operator-(const Point &b) const {
return {x - b.x, y - b.y};
}
// 重载乘法运算符,用于点与整数相乘
Point operator*(const int &b) const {
return {x * b, y * b};
}
// 重载异或运算符,用于计算两个向量的叉积
int operator^(const Point &b) const {
return x * b.y - y * b.x;
}
};
struct Line { // 定义线段结构体
Point p; // 线段的起点
Point q; // 线段的终点
};
vector<Line> lines;
int sgn(int x);
bool intersect(Line l1, Line l2);
bool onSegment(Point point, Line line);
int main() {
int n, cnt = 0;
cin >> n; // 线段数量
int x1, y1, x2, y2;
for (int i = 0; i < n; i++) {
cin >> x1 >> y1 >> x2 >> y2;
lines.push_back({{x1, y1}, {x2, y2}}); // 将线段添加到数组中
}
for (int i = 0; i < n; i++) // 双重循环遍历所有线段对,判断是否相交
for (int j = 0; j < i; j++)
if (intersect(lines[i], lines[j]))
cnt++; // 如果相交,则计数器加一
cout << cnt; // 输出相交线段对数
return 0;
}
int sgn(int x) {
if (x < 0) return -1;
if (x > 0) return 1;
return 0;
}
bool intersect(Line l1, Line l2) {
int d1 = sgn((l1.q - l1.p) ^ (l2.p - l1.p));
int d2 = sgn((l1.q - l1.p) ^ (l2.q - l1.p));
int d3 = sgn((l2.q - l2.p) ^ (l1.p - l2.p));
int d4 = sgn((l2.q - l2.p) ^ (l1.q - l2.p));
// 如果两线段在彼此的两侧,则相交
if (d1 * d2 < 0 && d3 * d4 < 0)
return true;
// 其中一个端点在另一条线段上,也视为相交
if (d1 == 0 && onSegment(l2.p, l1))
return true;
if (d2 == 0 && onSegment(l2.q, l1))
return true;
if (d3 == 0 && onSegment(l1.p, l2))
return true;
if (d4 == 0 && onSegment(l1.q, l2))
return true;
return false;
}
bool onSegment(Point point, Line line) { // 判断点是否在线段上
if (point.x >= min(line.p.x, line.q.x) &&
point.x <= max(line.p.x, line.q.x) &&
point.y >= min(line.p.y, line.q.y) &&
point.y <= max(line.p.y, line.q.y))
return true;
return false;
}
寻找凸包(Graham扫描法)
1 | |
点、向量相关
1 | |
maybe凸包相关
1 | |
直线相关
1 | |
圆相关
1 | |
快速幂取余
1 | |
快速打质数表
1 | |
单调栈
寻找左侧第一个比当前元素大的元素:从左到右遍历元素,构造单调递增栈(从栈顶到栈底递增) 一个元素左侧第一个比它大的元素就是将其「插入单调递增栈」时的栈顶元素。 如果插入时的栈为空,则说明左侧不存在比当前元素大的元素。
寻找左侧第一个比当前元素小的元素:从左到右遍历元素,构造单调递减栈(从栈顶到栈底递减) 一个元素左侧第一个比它小的元素就是将其「插入单调递减栈」时的栈顶元素。 如果插入时的栈为空,则说明左侧不存在比当前元素小的元素。
寻找右侧第一个比当前元素大的元素:从左到右遍历元素,构造单调递增栈(从栈顶到栈底递增) 一个元素右侧第一个比它大的元素就是将其「弹出单调递增栈」时即将插入的元素。 如果该元素没有被弹出栈,则说明右侧不存在比当前元素大的元素。
寻找右侧第一个比当前元素小的元素:从左到右遍历元素,构造单调递减栈(从栈顶到栈底递减) 一个元素右侧第一个比它小的元素就是将其「弹出单调递减栈」时即将插入的元素。 如果该元素没有被弹出栈,则说明右侧不存在比当前元素小的元素。
查找 「比当前元素大的元素」 就用 单调递增栈,查找 「比当前元素小的元素」 就用 单调递减栈。
从 「左侧」 查找就看 「插入栈」 时的栈顶元素,从 「右侧」 查找就看 「弹出栈」 时即将插入的元素。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57#include <cstdio>
#define MAX (300000+10)
int monoIncreaseStack(int height, int id);
void push(long long height, long long id);
long long pop();
struct student{
long long id;
long long height;
long long leftBigId, rightBigId; // 左侧第一个比当前元素的height大的数的id 右侧...
};
struct student stacks[MAX]; // 栈
struct student students[MAX]; // 所有的学生
int Top = -1;// 栈指针
int main() {
int t;
scanf("%d", &t);
while (t--){
int n;
Top = -1;
scanf("%d", &n);
for (int i = 0; i < n; ++i) { // 读取所有height,单调栈处理
long long height;
scanf("%lld", &height);
students[i].height = height;
students[i].id = i;
monoIncreaseStack(height, i);
}
while(Top != -1){
// 现在还在栈里的数的右侧都没有比它大的数
students[stacks[Top].id].rightBigId = n;
pop();
}
}
return 0;
}
int monoIncreaseStack(int height, int id){ // 当前元素大小height index为id
// 弹出所有比当前元素小的元素
while(Top!=-1 && height>=stacks[Top].height){
long long popId = pop();
students[popId].rightBigId = id; // id是popId右侧第一个比它大的元素
}
if(Top == -1){
students[id].leftBigId = -1; // id左侧没有比它大的元素
}else{
students[id].leftBigId = stacks[Top].id;
}
push(height, id); // 入栈
}
void push(long long height, long long id){
stacks[++Top].height = height; // 入栈成功
stacks[Top].id = id;
}
long long pop(){
return stacks[Top--].id; // 出栈成功
}
秦九韶算法/Horner 规则
\(A(x)=a_{n}x_{n}+a_{n−1}x_{n−1}+...+a_{1}x+a_{0}\) 在 \(x_{0}\) 处的值相当于 \(a_0+x_0(a_{1}+...+x_{0}(a_{n−1}+x_{0}a_{n}))\)
大数相乘
1 | |
随机数
1 | |
模逆元
模逆元:\(a×x≡1 (mod m)\)
如果p是一个质数,a是任意整数,且a不是p的倍数,那么a的模逆元可以表示为:\(a^{-1} \equiv a^{p-2} \ (\text{mod} \ p)\)
即 1
2
3
4
5
6
7
8
9
10long long qmi(long long mom, long long b, long long mod){ // 快速幂函数
long long res = 1;
while(b){
if(b & 1) res = res * mom % mod;
b >>= 1;
mom = mom * mom % mod;
}
return res;
}
x = qmi(a, MOD-2, MOD); //x是a在mod MOD下的逆元
MORE……
- 双指针 left 和 right