【学习经验】分光仪预习报告
实验器材

实验1 分光仪的调整
1 实验步骤
- 目测粗调
- 步骤:调节望远镜俯仰螺钉,目测望远镜垂直主轴,调节载物台下方3只螺钉伸出等长
- 目标现象:旋转平面镜180°前后均可见绿十字
- 望远镜的调整
- 调节望远镜聚焦于无限远(使望远镜接受平行光,叉丝分划板在物镜焦平面上)
- 依据:自准直原理
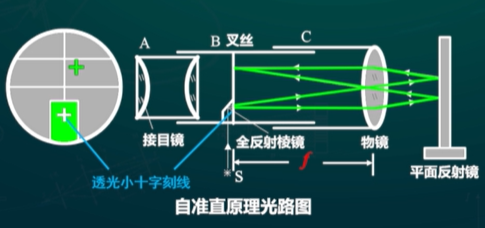
- 步骤:
- 将平面镜置于载物台上,平面镜镜面与载物台上径线OA平行
- 调节目镜与叉丝分划板之间距离(使用目镜调节手轮)至叉丝清晰
- 调节物镜与叉丝之间距离至绿十字清晰
- 将平面镜置于载物台上,平面镜镜面与载物台上径线OA平行
- 目标现象:绿十字与叉丝无视差(像不模糊)
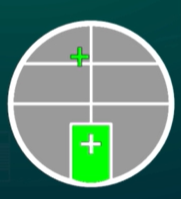
- 依据:自准直原理
- 调望远镜光轴垂直于主轴(使观察平面与刻度盘平行)
- 方法:半调法(逐次逼近调节法)
- 步骤:
- 调节望远镜俯仰螺钉,使绿十字与上叉丝的偏离减少一半
- 调节载物台螺钉b或c,使绿十字与上叉丝重合
- 旋转载物台180°,重复以上步骤直到正反两面绿十字均与上叉丝重合
- 注意:
- 调好后望远镜的焦距和俯仰不可再动
- 调望远镜还是载物台?
- 若转了180°之后绿十字一上一下,调载物台
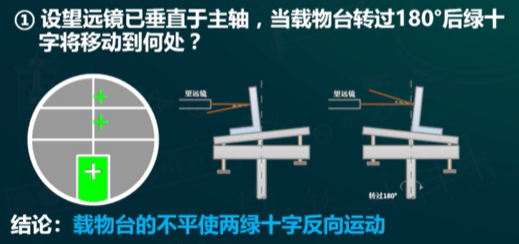
- 若转了180°之后绿十字高度没动,调望远镜
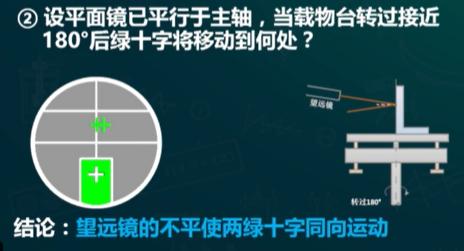
- 若转了180°之后绿十字一上一下,调载物台
- 目标现象:反射镜正反两面绿十字均与上叉丝重合
- 调节望远镜聚焦于无限远(使望远镜接受平行光,叉丝分划板在物镜焦平面上)
- 平行光管的调整
- 调平行光管聚焦于无限远
- 依据:透镜成像原理(狭缝处于透镜平面时出射平行光)
- 方法:拿下平面镜,打开外置光源,前后移动狭缝套筒,调节平行光管物距
- 目标现象:狭缝像与叉丝无视差(狭缝像边缘清晰)
- 调平行光管光轴处置于主轴
- 原理:平行光管与望远镜共轴,则其与主轴垂直
- 方法:调节平行光管俯仰螺钉,使狭缝像中点与中心叉丝重合;或旋转狭缝套筒90°,使狭缝像的固定边与中心叉丝重合
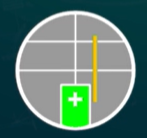
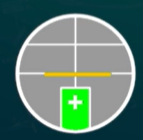
- 目标现象:狭缝像中点与中心叉丝重合
- 调平行光管聚焦于无限远
- 三棱镜的调整(使待测光路平面平行于观察平面)
- 原理:自准直原理(使望远镜与两光学面垂直)
- 步骤:
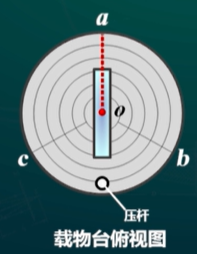
- 如图放置三棱镜,保证两边与平台上径线平行(\(AB//ob,AC//oc\))
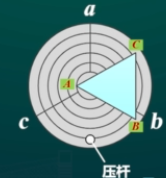
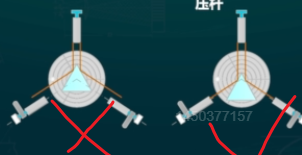
- 望远镜对转光学面(AB),调整另一光学面(AC)平行径线下的载物台螺钉(c),使绿十字与上叉丝重合
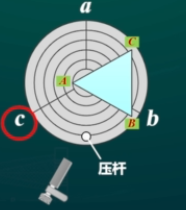
- 望远镜对准光学面(AC),调整另一光学面(AB)平行径线下的载物台螺钉(b),使绿十字与上叉丝重合
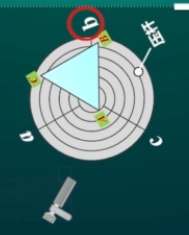
- 如图放置三棱镜,保证两边与平台上径线平行(\(AB//ob,AC//oc\))
- 目标现象:两光学面的绿十字均与上叉丝重合
实验2 三棱镜顶角的测量
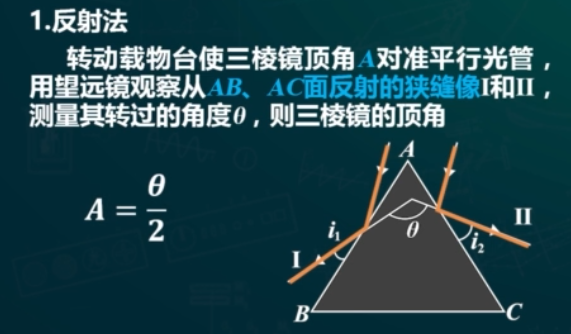
- 读第一个数(望远镜在AB左边),左边游标读数 \(\alpha_1\),右边游标读数 \(\beta_1\);望远镜转到AC右边,左边游标读数 \(\alpha_2\),右边游标读数 \(\beta_2\)
- 重复六次
- 望远镜转过角度 \(\theta = \frac{\alpha_{2}-\alpha_{1}+\beta_{2}-\beta_{1}}{2}\)
- 三棱镜顶角 \(A = \frac{\theta}{2}\)
实验3 最小偏向角法测量棱镜折射率
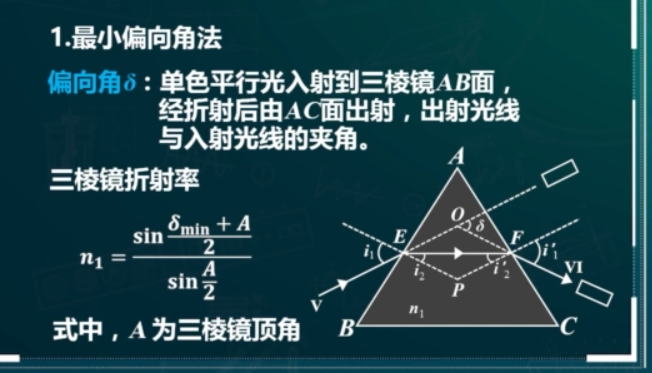
- 如图放置三棱镜,旋转望远镜找到平行光。用望远镜在AC面观察折射光线,沿某方向缓慢转动载物平台(改变入射角),可看到谱线随平台转动向一个方向移动,当移到某个位置时突然折返。旋转望远镜使平行光出现在叉丝中间,在该位置有左边游标读数 \(\alpha_1\),右边游标读数 \(\beta_1\);拿下三棱镜,旋转望远镜使叉丝出现在中间(望远镜在入射光对面),在该位置有左边游标读数 \(\alpha_2\),右边游标读数 \(\beta_2\)。
- 重复三次
- \(\theta_{1} = \alpha_2-\alpha_1,\ \theta_2=\beta_2-\beta_1,\ \delta_{min}=\frac{\theta_{1}+\theta_{2}}{2}\)
- \(n_{1}=\frac{sin\frac{\delta_{min}+A}{2}}{sin \frac{A}{2}}\)
实验4 掠入射法测量棱镜折射率
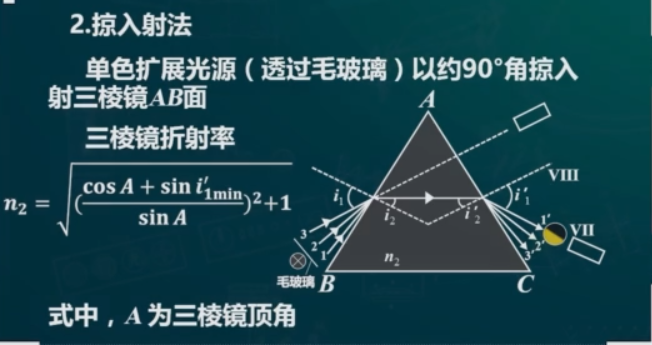
- 放置三棱镜使三棱镜一个平面与平行光管垂直
- 整体移动分光仪使光源在一个平面的延长线上
- 转动望远镜,在AC面寻找半明半暗交界线,在该位置有左边游标读数 \(\alpha_1\),右边游标读数 \(\beta_1\);
- 转动望远镜(在大概AC面的垂直位置),使绿十字与叉丝的竖直线重合,在该位置有左边游标读数 \(\alpha_2\),右边游标读数 \(\beta_2\)。
- 重复三次
- \(\theta_{1} = \alpha_2-\alpha_1,\ \theta_2=\beta_2-\beta_1,\ \delta_{min}=\frac{\theta_{1}+\theta_{2}}{2}\)
- \(n_{2}=\sqrt{(\frac{cosA+sin\delta_{min}}{sinA})^{2}+1}\)
【学习经验】分光仪预习报告
http://example.com/2024/10/25/jwsy-fenGuangYi/