【数据结构】ds笔记7-排序

本篇笔记总结DSPv2b_8(排序) for student内的相关内容。没有配图不是因为不抽象，而是因为太抽象，照片没用，建议直接看PPT的动画。最后，本人学艺不精，只是一边看着ppt一边敲敲改改，如有疏漏，欢迎提出喵~o( =∩ω∩= )m

1 排序的基本概念

  1. 排序的定义

    对于含有n个记录的序列{ R1, R2, ..., Rn}, 对应的关键字序列为{k1, k2, ..., kn}, 确定一种置换关系 s(1), s(2), ..., s(n)，使得关键字序列满足： ks(1) ≤ ks(2) ≤ ... ≤ ks(n) 或者 ks(1) ≥ ks(2) ≥ ... ≥ ks(n)，相应文件成为按关键字值有序的文件{ Rs(1), Rs(2), ... , Rs(n)}，这一过程称为排序。简单来讲，就是将一个按值任意的数据元素序列转换为一个按值有序的数据元素序列。

  2. 排序的功能

    1. 能够将记录按关键字值任意排列的数据文件转换为一个记录按关键字值有序排列的数据文件。或者能够将一个按值任意排列的数据元素序列转换为一个按值有序排列的数据元素序列。
    2. 能够提高查找的时间效率。

  3. 排序的分类（按存储器的结构分）

    1. 内排序

      参加排序的数据量不大，以致于能够一次将参加排序的数据全部装入内存实现排序。

    2. 外排序

      当参加排序的数据量很大，以致于不能够一次将参加排序的数据全部装入内存，排序过程中需要不断地通过内存与外存之间的数据交换达到排序目的。

  4. 排序的性能

    1. 时间性能

      排序过程中元素之间的比较次数与元素的移动次数。

    2. 空间性能

      除了存放参加排序的元素之外，排序过程中所需要的其他辅助空间。

    3. 稳定性

      对于值相同的两个元素，排序前后的先后次序不变，则称该方法为稳定性排序方法，否则，称为非稳定性排序方法。

  5. 名词解释——趟

    将具有n个数据元素(关键字)的序列转换为一个按照值的大小有序排列（如从小到大）的序列，通常要经过若干趟(Pass)。

2 插入(insert)排序法

  1. 核心思想

    第i趟排序将序列的第i+1个元素插入到一个大小为i、且已经按值有序的子序列(ki-1,1, ki-1,2, …, ki-1,i)的合适位置，得到一个大小为i+1、且仍然按值有序的子序列(ki,1, ki,2, …, ki,i+1)。其中ki,j表示第i趟排序结束时序列的第j个元素，1≤i≤n-1，1≤j≤n

  2. 算法

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    void insertSort(keytype k[ ],int n){
        int i, j;
        keytype temp;
        for(i=1;i<n;i++){
            temp=k[i];
            for(j=i-1; j>=0 && temp<k[j]; j--) 
            	k[j+1]=k[j];
            k[j+1]=temp;
    	}
    }

  3. 思考题

    1. 排序的时间效率与什么直接有关？

      主要与排序过程中元素之间的比较次数直接有关。

    2. 若原始序列为一个按值递增的序列，则排序过程中一共要经过多少次元素之间的比较？

      由于每一趟排序只需要经过一次元素之间的比较就可以找到被插入元素的合适位置，因此，整个n-1趟排序一共要经过n-1次元素之间的比较。

    3. 若原始序列为一个按值递减的序列，则排序过程中一共要经过多少次元素之间的比较？

      由于第i趟排序需要经过i次元素之间的比较才能找到被插入元素的合适位置,因此,整个n-1趟排序一共要经过 \[ \sum_{i=1}^{n-1}i = n(n-1)/2 \] 次元素之间的比较。

  4. 时间复杂度：最差O(n2) 最佳O(n) 平均O(n2)

    空间复杂度：O(1)

    稳定

3 选择(select)排序法

  1. 核心思想

    第i趟排序从序列的后n-i+1个元素中选取一个值最小的元素，将其置于该n-i+1个元素

    的最前面。

  2. 算法

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    void selectSort(keytype k[ ],int n){
        int i, j, d;
        keytype  temp;
        for(i=0;i<n-1;i++){
        	d=i;		// 寻找值最小的元素并记录其位置
        	for(j=i+1;j<n;j++)
        		if(k[j]<k[d])
        			d=j;
            if(d!=i){    
                /* 最小值元素非未排序元素的第一个元素时 */
                temp=k[d] ;
                k[d]=k[i];
                k[i]=temp;
            }
        }
    }

  3. 思考题

    若原始序列为一个按值递增的序列，则排序过程中一共要经过多少次元素之间的比较？若原始序列为一个按值递减的序列，则排序过程中要经过多少次元素之间的比较？

    无论原始序列为什么状态，第i趟排序都需要经过n-i次元素之间的比较，因此，整个排序过程中元素之间的比较次数为 \[ \sum_{i=1}^{n-1}(n-i) = n(n-1)/2 \] 即选择排序法的元素之间的比较次数与原始序列中元素的分布状态无关。

  4. 时间复杂度：O(n2)

    空间复杂度：O(1)

    不稳定

4 冒泡(bubble)排序法

  1. 核心思想

    第i趟排序对序列的前n-i+1个元素从第一个元素开始依次作如下操作:相邻的两个元素比较大小，若前者大于后者,则两个元素交换位置，否则不交换位置。

    即值大的元素往后“沉”，值小的元素向前“浮”。

    效果：该n-i+1个元素中最大值元素移到该n-i+1个元素的最后。

  2. 算法

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    void bubbleSort(keytype k[ ],int n){
        int i, j, flag=1;
        keytype temp;
        for(i=n-1; i>0 && flag==1; i--){
            flag=0;                        /* 每趟排序前标志flag置0 */ 
            for(j=0; j<i; j++) 
                if(k[j]>k[j+1]){
                    temp=k[j];
                    k[j]=k[j+1];
                    k[j+1]=temp;  /* 交换两个元素的位置 */     
                    flag=1;              /* 标志flag置1 */ 
                }
        }
    }

  3. 泡排序方法比较适合于参加排序的序列的原始状态基本有序的情况。

  4. 时间复杂度：一般O(n2) 最少O(n)

    空间复杂度：O(1)

    稳定

5 谢尔(Shell)排序法

  1. 核心思想

    首先确定一个元素的间隔数gap。将参加排序的元素按照gap分隔成若干个子序列（即分别把那些位置相隔为gap的元素看作一个子序列），然后对各个子序列采用某一种排序方法进行排序；此后减小gap值，重复上述过程，直到gap<1。

    一种减小gap的方法： gap1 = ⌊n/2⌋; gapi = ⌊gapi-1/2⌋ i=2,3,...

  2. 算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
// 1 利用冒泡排序
// 1.1 法1
void shellSort(keytype k[ ],int n){
    int i, j, flag, gap=n;
    keytype temp; 
    while(gap > 1){
        gap = gap/2;
        do{
            flag = 0;                  /* 每趟排序前,标志flag置0 */ 
            for(i=0; i<n–gap; i++){
                j = i+gap;
                if(k[i] > k[j]){
                    temp = k[i];
                    k[i] = k[j];
                    k[j] = temp;
                    flag = 1;  
                }
            }
        }while(flag!=0);
    }
}
// 1.2 法2
void shellSort(int v[ ], int n){		//from K & R
	int gap, i, j, temp;
	for(gap=n/2; gap>0; gap/=2)
		for(i=gap; i<n; i++)
			for(j=i-gap; j>=0 && v[j]>v[j+gap]; j -= gap){
                temp = v[j];
                v[j] = v[j+gap];
                v[j+gap] = temp;
            }
}

// 2 利用插入排序
void shellSort(keytype k[ ],int n){
    int i, j, gap = n;
    keytype temp; 
    while(gap>1){
        gap = gap/2;
        
        // 使用插入排序实现子序列排序
        for(i=gap; i<n; i++){
            temp = k[i];
            for (j=i; j>=gap && k[j-gap]>temp; j-=gap)
            	k[j] = k[j-gap];
            k[j] = temp;
        }
    }
}

  1. 时间复杂度：O(nlog2n)与O(n2)之间，通常＜O(n2)

    空间复杂度：O(1)

    不稳定

6 堆(Heap)排序法

  1. 堆的定义

    n个元素的序列(k1, k2, … , kn)，当且仅当满足 \[ (1)\begin{cases} \begin{aligned} k_i \ge k_{2i}\\ k_i \ge k_{2i+1} \end{aligned} \end{cases} \quad 或者\quad (2)\begin{cases} \begin{aligned} k_i \le k_{2i}\\ k_i \le k_{2i+1} \end{aligned} \end{cases}\\ i=1, 2, 3, …, \lfloor n/2 \rfloor \] 称该序列为一个堆积(heap)，简称堆。称满足条件(1)的堆为大顶推，称满足条件(2)的堆为小顶堆。

    例：一个大顶堆：50 23 41 20 19 36 4 12 18

    • 堆是一棵完全二叉树，二叉树中任何一个分支结点的值都大于或者等于它的孩子结点的值，并且每一棵子树也满足堆的特性。

  2. 排序的核心思想

    第i趟排序将序列的前n-i+1个元素组成的子序列转换为一个堆积，然后将堆的第一

    个元素与堆的最后那个元素交换位置。

  3. 排序步骤

    1. 将原始序列转换为第一个堆。
    2. 将堆的第一个元素与堆积的最后那个元素交换位置。(即“去掉”最大值元素）
    3. 将“去掉”最大值元素后剩下的元素组成的子序列重新转换一个新的堆。
    4. 重复上述过程的第2至第3步n-1次。

  4. 调整子算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
/*
功能：向下调整结点i的位置，使得其祖先结点值都比其大。如果一棵树仅根结点i不满足堆条件，通过该函数可将其调整为一个堆。
K :序列
i :被调整的二叉树的根的序号
n :被调整的二叉树的结点数目
*/
void adjust(keytype k[ ], int i, int n){
    int j;
    keytype temp;
    temp = k[i];
    j = 2*i+1;
    while(j < n){
        if(j+1<n && k[j]<k[j+1])
        	j++;
        if(temp < k[j]) {
            k[(j-1)/2] = k[j];
            j = 2*j+1;
        }else
           	break;
    }
    k[(j-1)/2] = temp;
}

  1. 建初始堆

    从二叉树的最后那个分支结点(编号为i=⌊n/2-1⌋)开始，依次将编号为i的结点为根的二叉树转换为一个堆，每转换一棵子树，做一次i减1，重复上述过程，直到将i=0的结点为根的二叉树转换为堆。

  2. 堆排序算法

1
2
3
4
5
6
7
8
9
10
11
12
void heapSort(keytype k[ ],int n){
    int i,
    keytype temp;
    for(i=n/2-1; i>=0; i--)		// 建初始堆积
    	adjust(k, i, n);
    for(i=n-1; i>=1; i--){		// 具体排序
        temp = k[i];
        k[i] = k[0];
        k[0] = temp;
        adjust(k, 0, i);
    }
}

  1. 时间复杂度：O(nlog2n)

    空间复杂度：O(1)

    不稳定

7 二路归并(Merge)排序法

  1. 二路归并：将两个位置相邻、并且各自按值有序的子序列合并为一个按值有序的子序列的过程称为二路归并。 \[ \underbrace{(K_s, K_{s+1}, K_{s+2}, ..., K_u)(K_{u+1}, K_{u+2}, K_{u+3},..., K_v)}_{\text{Xs, Xs+1, Xs+2, Xs+3,...,Xv}}\\ 其中K_s \le K_{s+1} \le K_{s+2} \le ... \le K_u \\ K_{u+1} \le K_{u+2} \le K_{u+3} \le ... \le K_v \\ X_s \le X_{s+1} \le X_{s+2} \le X_{s+3} \le ... \le X_v \]

  2. 合并算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
void merge(keytype x[ ], keytype tmp[ ], int left, int leftend, int rightend){     
    int i = left, j = leftend+1, q = left;
    while(i<=leftend && j<=rightend)
    	if(x[i] <= x[j]) 
    		tmp[q++] = x[i++];
    	else
    		tmp[q++] = x[j++];
    while(i <= leftend)		// 复制第一个子序列的剩余部分
    	tmp[q++] = x[i++];
    while(j <= rightend)	// 复制第二个子序列的剩余部分
    	tmp[q++] = x[j++];
    for(i=left; i<=rightend; i++)		// 将合并后内容复制回原数组
    	x[i] = tmp[i];
}

  1. 核心思想

    第i趟排序将序列的⌊n/2i-1⌋个长度为2i-1的按值有序的子序列依次两两合并为⌊n/2i⌋个长度为2i的按值有序的子序列。

  2. 算法（本质上是分治算法）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
void mergeSort(keytype k[ ],int n){
	keytype *tmp;
    tmp = (keytype *)malloc(sizeof(keytype) * n);
    if(tmp != NULL) {
        mSort(k, tmp, 0, n-1);
        free(tmp);
    } 
    else
        printf("No space for tmp array!!!\n");
}
void mSort(keytype k[], keytype tmp[], int left, int right){
    int center;
    if(left < right){
        center = (left+right)/2;
        mSort(k, tmp, left, center);
        mSort(k, tmp, center+1, right);
        merge(k, tmp, left,center, right);
    }
}

  1. 时间复杂度：O(nlog2n)（不依赖于原式数据输入情况）

    空间复杂度：O(n)

    稳定

8 快速(Quick)排序法（即qsort）

  1. 核心思想

    从当前参加排序的元素中任选一个元素(通常称之为分界元素pivot)与当前参加排序的那些元素进行比较，凡是小于分界元素的元素都移到分界元素的前面，凡是大于分界元的元素都移到分界元素的后面，分界元素将当前参加排序的元素分成前后两部分，而分界元素处在排序的最终位置。然后，分别对这两部分中大小大于1的部分重复上述过程，直到排序结束。

  2. 算法步骤

    1. 算法中用到的变量：

      left：当前参加排序的那些元素的第一个元素在序列中的位置，初始值为0。

      right：当前参加排序的那些元素的最后那个元素在序列中的位置, 初始值为n-1。

      i,j：两个位置变量，初始值分别为left与right+1。

    2. 步骤：

      1. 反复执行动作i=i+1，直到K[left]≤K[i]或者i=right。

        反复执行动作j=j-1，直到K[left]≥K[j]或者j=left。

      2. 若i<j，则K[i]与K[j]交换位置，转到第1步。

      3. 若i≥j，则K[left]与K[j]交换位置,到此,分界元素K[left]的最终位置已经确定(j)，然后对被K[left]分成的两部分中个数大于1 的部分重复上述过程，直到排序结束。

  3. 算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
// way1
// 主算法
void quickSort(keytype k[],int n){
	quick(K, 0, n-1);
}
void quick(keytype k[ ],int left,int right){
    int i, j;
    keytype pivot;
    if(left < right){
        i = left;
        j = right+1;
        pivot = k[left];
        while(1){ 
            while(k[++i]<pivot && i!=right) { }
            while(k[--j]>pivot && j!=left) { }
            if(i < j)
            	swap(&k[i], &k[j]);  /*交换K[i]与K[j]的内容*/
            else
            	break;
        }
        swap(&k[left], &k[j]);      /*交换K[s]与K[j]的内容*/
        quick(k, left, j-1);       /* 对前一部分排序 */
        quick(k, j+1, right);       /* 对后一部分排序 */
    }
}
void swap(keytype *x, keytype *y){
    keytype temp;
    temp = *x;//取内容交换
    *x = *y;
    *y = temp;
}

// way2 BY K&R
// 主算法
void quickSort(keytype k[],int n){
       qsort(k, 0, n-1);
}
void qsort(keytype v[ ],int left, int right){
    int i, last;
    if(left >= right)
        return;
    swap(v, left, (left+right)/2);		//move partition elem to v[0]
    last = left;
    for(i=left+1; i<=right; i++)		//partition
        if(v[i] < v[left])
            swap(v, ++last, i);
    swap(v, left, last);		//restore partition elem
    qsort(v, left, last);  
    qsort(v, last+1, right);
}
void swap(keytype v[ ],int i, int j){
    keytype tmp;
    tmp = v[i];
    v[i] = v[j];
    v[j] = tmp;
 }

  1. 不稳定

    最差情况：时间复杂度：O(n2) 空间复杂度：O(n)

    最佳情况：时间复杂度：O(nlog2n) 空间复杂度：O(log2n)

    平均情况：时间复杂度：O(nlog2n) 空间复杂度：O(log2n)

9 总结

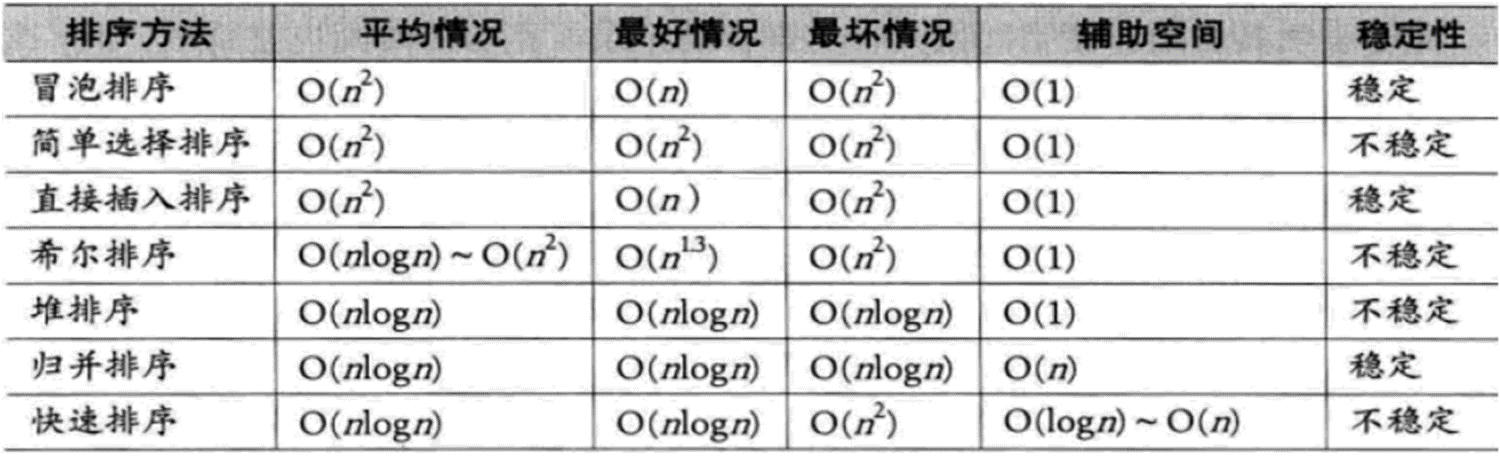
  1. 从算法性质来看：

    1. 简单算法：冒泡、选择、插入
    2. 改进算法：谢尔、堆、归并、快速

  2. 从时间复杂度来看：

    1. 平均情况：后3种改进算法 > 谢尔 (远)> 简单算法
    2. 最好情况：冒泡和插入排序要更好一些
    3. 最坏情况：堆和归并排序要好于快速排序及简单排序

  3. 从空间复杂度来看：

    归并排序有额外空间要求，快速排序也有相应空间要求，堆排序则基本没有。

  4. 从稳定性来看：

    除了简单排序，归并排序不仅速度快，而且还稳定

10 *桶(Bucket)排序法（计数排序）

  1. 核心思想

    假设a1,a2,…,an由小于M的正整数组成，桶排序的基本原理是使用一个大小为M的数组C(初始化为0，称为桶bucket)，当处理ai时，使C[ai]增1。最后遍历数组C输出排序后的表。（感觉和Hash是一个感觉）

  2. 算法

1
2
3
4
5
6
7
8
void bucketSort(int K[ ], int n){
	int C[M]={0}, i, j;
    for(i=0; i<n; i++)
    	C[K[i]]++;
    for(i=0,j=0; i<M; i++)
        if(C[i])
            K[j++] = i;
}

  1. 时间复杂度：O(M+N)

    不稳定

学习经验 > 数据结构
#学习经验
【数据结构】ds笔记7-排序
http://example.com/2024/05/13/LE-ds7/
Author
John Doe
Posted on
May 13, 2024
Licensed under