【数据结构】ds笔记6-查找

本篇笔记总结DSPv2b_7(查找) for student内的相关内容。（说到底为什么不先讲图而是先讲查找啊kuso）。依旧，大部分内容照搬ppt，但是5 B-树和B+树中的5.0 说在前面是本人依靠智谱清言写出来的（理直气壮）。起因是问了两位学长都表示“我不道啊”，但本人觉得这问题摆在那里实在难受，只得求助AI sama。

以及3.3 插值查找、3.4 斐波那契查找和4.5倒排索引暂时只有一个标题，大概会在本周内进行更新。再以及，本人的ds笔记中的插图大部分是在是太过不好看，本人争取在下学期开学之前（xd）进行一个大更新。再再以及，祝各位期中顺利。再再再以及，昆明好玩，云南好玩，洋芋和烤蚂蚱都好吃，下辈子一定要投胎到云南！再再再再以及，夏天到了，天气热了，太阳晒了，蚊虫多了，我要躲进屋子里了（卒）

最后，本人学艺不精，只是一边看着ppt一边敲敲改改，如有疏漏，欢迎提出喵~o( =∩ω∩= )m

1 Trie树

1.1 简介

1. 在二叉树遍历中通常是通过比较整个键值来进行的，即每个结点包含一个键 值，该键值与要查找的键值进行比较从而在树中寻找正确的路径。而用键值的一部分来确定查找路径的树称为trie树（它来源于retrieval，也可称为字典树）。在访问速度要求很高的系统中，如拼写检查、词频统计中，Trie结构是一种非常好的选择。
2. 主要应用：
   1. 信息检索
   2. 用来存储英文字符串，特别是大规模的英文词典（在自然语言理解软件中 经常用到，如词频统计、拼写检查）

1.2 结构

1. 两个原则

   1. 键值由固定的字符序列组成（如数字或字母），如Huffman码(只由0,1组成)、英文单词（只由26个字母组成）；
   2. 对应结点的分层标记。

2. 结构典型应用：字典树

   1. 字典树每个内部结点都有26个子结点——多叉树
   2. 树的高度为最长单词长度

3. 构造示例

// 一种用于描述单词的trie结构定义
struct tnode{	// word tree 
    char isword;	// is or not a word
    char isleaf;	// is or not a leaf node
    struct tnode *ptr[26];
};

// 基于trie结构的单词树的构造
void wordTree(struct tnode *root, char *w){
    // install w at or below p
    struct tnode *p;
    for(p=root; *w != '\0'; w++){
        if(p->ptr[*w-'a'] == NULL){
            p->ptr[*w-'a'] = talloc();		// 自己写的函数(tree alloc)
            p->isleaf = 0;
        }
        p = p->ptr[*w-'a'];
    }
    p->isword = 1;
}

1.3 例：查家谱

1. 题目：同姓氏中国人见面常说的一句话是“我们五百年前可能是一家”。从当前目录下的文件in.txt中读入一家谱，从标准输入读入两个人的名字（两人的名字肯定会在家谱中出现），编程查找判断这两个人相差几辈，若同辈，还要查找两个人共同的最近祖先以及与 他（她）们的关系远近。假设输入的家谱中每人最多有两个孩子，例如下图是根据输入形成的一个简单家谱。若要查找的两个人是wangqinian和wangguoan，从家谱中可以看出两人相差两辈；若要查找的两个人是wangping和wanglong，可以看出两人共同的最近祖先是wangguoan，和两人相差两辈。

   

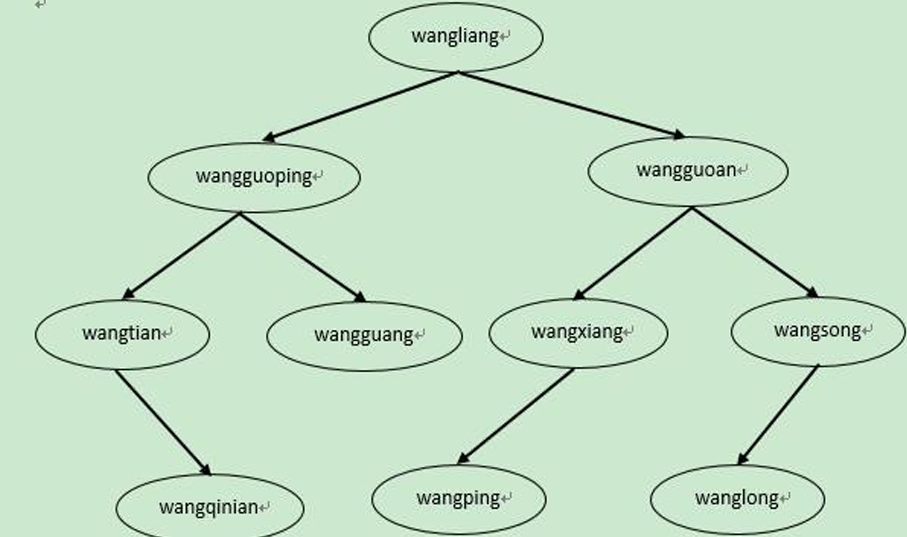
2. 输入示例：

   假设家谱文件中内容为：

   6

   wangliang wangguoping wangguoan

   wangguoping wangtian wangguang

   wangguoan wangxiang wangsong

   wangtian wangqinian NULL

   wangxiang wangping NULL

   wangsong wanglong NULL

   从标准输入读取：

   wangping wanglong

3. 输出示例

   wangguoan wangping 2

   wangguoan wanglong 2

4. 说明：wangping和wanglong共同的最近祖先是 wangguoan，该祖先与两人相差两辈。

5. 问题分析与设计

   1. 构造家谱（树）：如何利用结点之间的（父子）关系构造树（家谱）。一个简单直接的方法是：

      结点插入法构造。利用前序遍历找到相应的父结点，然后将子结点插入。该方法简单，对结点顺序要求不高（但父结点要在子结点前输入）；该方法的核心就是结点查找。

root = NULL;
for(i=0; i<n; i++){ //create a family tree
    fscanf(in,"%s%s%s", name0, name1, name2);
    root = insert(root, name0, name1, name2);
}

2. 查家谱：实际上就是查找相应结点。如果能得到结点至根的路径信息，就很容易计算出两个结点关系（如是否同辈、相差几辈、共同的祖先等）。

   如何在查找一个结点时得到其（从根结点至该结点的）路径信息：

   ①在前序查找过程中设置一个栈来保存路径信息；

   ②一个简单的方法：为每个结点增加一个指向父结点的指针信息，这样在找到结点的同时，也就获得了相应的路径。

2 查找的基本概念

2.1 一些概念

1. 属性：描述一个客体某一方面特征的数据信息。
2. 记录：反映一个客体数据信息的集合（属性的集合），就是数据元素。
3. 查找表：具有相同属性定义的记录的集合。
4. 关键字：区分不同记录的属性或属性组（或组合）。
   1. 主关键字(Primary Key)：可以唯一的表示一个记录。
   2. 次关键字

2.2 两种类型：静态查找表和动态查找表

1. 静态查找表(只进行查找操作)

   如果只在查找表中确定某个特定记录是否存在或检索某个特定记录的属性，此类查找表为静态查找表(Static Search Table)

2. 动态查找表（查找同时可能有插入或者删除操作）

   如果在查找表中需要插入不存在的数据元素（记录）或需要删除检索到的数据元素（记录），此类查找表为动态查找表(Dynamic Search Table)

3 顺序表的查找

3.1 折半查找

1. 思路

   1. 将要查找的关键字值与当前查找范围内位置居中的记录的关键字的值进行比较。
   2. 若匹配，则查找成功，给出被查到记录在查找表中的位置，查找结束。
   3. 若要查找的关键字值小于位置居中的记录的关键字值，则到当前查找范围的前 半部分重复上述查找过程，否则，到当前查找范围的后半部分重复上述查找过 程，直到查找成功或者失败。
   4. 若查找失败，则给出错误信息（如：-1）。

2. 变量含义

   • n：有序连续顺序查找表中记录的个数

   • low：当前查找范围内第一个记录在查找表中的位置

   • high：当前查找范围内最后一个记录在查找表中的位置

   • mid：当前查找范围内位置居中的记录在查找表中的位置。

     mid = (low + high) / 2

3. 算法

   1. 递归算法

// 算法的调用方式
low = 0;
high = n-1;
pos = binsearch2(KEY, low, high, k);

// 算法
int binsearch2(keytype key[], int low, int high, keytype k){
    int mid;
    if(low>high)	// 查找失败，返回-1。如有要求做插入操作，就在Low的位置
        return -1;
    else{ 
        mid = (low+high)/2;		// 取中
        if(k == key[mid])		// 找到
            return mid;
        else
            if(k < key[mid])// 要找的元素小于中间元素，范围缩半到前半部分
                return binsearch2(key, low, mid–1, k);
            else // 要找的元素大于中间元素，范围缩半到后半部分
                return  binsearch2(key, mid+1, high, k);
} 

  2. 非递归算法

int binsearch(keytype key[], int n, keytype k){
// 注意区分于递归算法的形式参数
	int low=0, high=n-1, mid;
	while (low <= high) {		// 查找结束的条件low >high    
    	mid = (low+high)/2;
    	if(k == key[mid])
        	return mid;		// 查找成功
    	if(k > key[mid])
        	low = mid+1;		// 准备查找后半部分
    	else
        	high = mid–1;		// 准备查找前半部分
    }
	return -1;				// 查找失败
}

4. 判定树

   若把当前查找范围内居中的记录的位置作为根结点，前半部分与后半部分记录的位置分别构成根结点的左子树与右子树,则由此得到一棵称为“判定树”的二叉树，利用它来描述折半查找的过程。

   

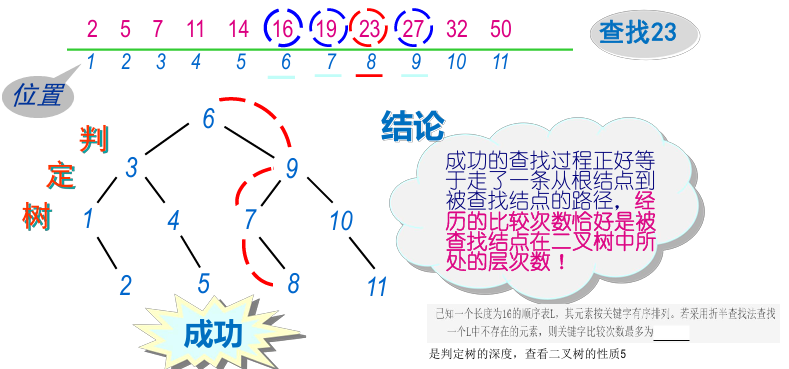
5. 平均查找长度ASL

   

6. 优点：

   1. 查找原理和过程简单，易于理解。
   2. 查找的时间效率较高

7. 缺点：

   1. 要求查找表中的记录按照关键字值有序排列（为了保持数据集为排序顺序数据集，在数据集中插入和删除记录时需要移动大量的其它记录）
   2. 对于查找表，只适用于有序连续顺序表

8. 使用场景：

   静态查找表；数据元素按值有序排列；采用顺序存储结构

9. 对于动态查找表，元素没有查找到时通常要进行插入操作，基于折半查找算法，如何获取元素的插入位置？

int insertElem(ElemType list[ ], ElemType item){
    int i=0, j;
    if (N == MAXSIZE)
		return -1; 
    i = searchElem(list, item);		// 寻找item的合适位置     
    for(j=N-1; j>=i; j--)
        list[j+1] = list[j];
    list[i] = item;					// 将item插入表中
    N++;
    return 1;
}
int searchElem(ElemType list[ ], ElemType item){
    int low=0, high=N-1, mid;
    while(low <= high){
        mid = (high + low) / 2;
			if(item < list[mid])
				high = mid – 1;
			else if(item > list[mid])
				low = mid + 1;
			else
				return (mid);
    }
    return low ;
}

3.2 链接查找表的查找

1. 适合动态查找表，但查找效率低

2. 链节点构造：

   key是关键字值，rec是记录的存储位置

3. 算法

struct node{
    keytype key;
    rectype rec;
    struct node *link;
};
// 从链表的入口指针开始，依次查找每个链结点
struct node *search(struct node *p, keytype k){    
	for(; p!=NULL; p=p->link)
		if(p->key==k)
			return p;		// 查找成功
	return NULL;		// 查找失败
}

3.3 *插值查找(Interpolation Search)

3.4 *斐波那契查找(Fibonacci Search)

4 索引

4.1 索引的基本概念

1. 索引：记录关键字值与记录的存储位置之间的对应关系。
2. 索引文件（建立了索引的文件）：由基本数据与索引表两部分组成的数据集称为索引文件。
3. 索引表的特点
   1. 一般由基本数据表经处理产生；
   2. 表项按关键字值有序排列。

4.2 稠密索引

1. 特点：基本数据中的每一个记录在索引表中都占有一项。
2. 在稠密索引文件中查找一个记录存在与否的过程是直接查找索引表。

4.3 非稠密索引——分块索引

1. 特点：将文件的基本数据中记录分成若干块(块与块之间记录按关键字值有序, 块内记录是否按关键字值有序无所谓),索引表中为每一块建立一项。

2. 在非稠密索引(分块)文件中查找一个记录存在与否的过程是：先查找索引表(确定被查找记录所在块)，然后在相应块中查找被查记录存在与否。

4.4 多级索引

当索引文件本身非常庞大时, 可以把索引文件再分块, 建立索引文件的索引, 形成树形结构的多级索引结构。

4.5 *倒排索引

5 B-树和B+树

5.0 说在前面

我在看B-树（B树）和B+树的ppt时看着看着就晕了，为什么B树的叶结点不包含任何关键字信息，B-树和B+树的区别中的第二点是什么意思，特别的，B树节点中的recptr[M+1]究竟指向哪里。想要搞清这些问题，我们首先要搞清B树究竟是用来干什么的。

智谱清言告诉我，“B树是一种自平衡的树数据结构，它设计用于在磁盘存储或其他直接访问的辅助存储设备上高效地管理和访问大量数据。B树的节点通常对应于磁盘上的一个块，因此它可以减少磁盘I/O操作，提高数据检索的效率”。也就是说，B树的结点最终连接的并不是那堆key，那些key只是数据记录们的一个昵称，就像学号和学生本人一样。我们把数据记录们”翻译“成一个个key，再把每个key和数据记录的地址绑定在一起，这样我们就能够通过对key进行操作来操作数据记录了。在我看来，我们可以把B树和Hash表进行类比，B树就是变成了树的Hash表。以上，我们可以解决刚刚提出的问题：

1. B树节点中的recptr[i]究竟指向哪里？

   它指向了key[i]对应的那堆数据记录，这些数据记录可能存储在磁盘上，也可能存储在内存中，取决于具体的B树实现和应用程序。

2. 为什么B树的叶结点不包含任何关键字信息？

   因为因为B树中的所有“有用的信息”（即关键字和对应的数据记录）都存放在数组key和数组recptr里。

3. B树和B+树的区别中的第二点是什么意思？

   提到的这一点区别是“B-树的每个分支结点中含有指向关键字值对应记录的指针，而B+树只有叶结点有指向关键字值对应记录的指针”。

   这句话的意思是，B树的每个分支结点都有recptr，指向key值对应的数据记录。而B+树的非叶结点的指针仅用于引导搜索过程，不指向key值对应的数据记录；只有其叶结点的指针指向key值对应的数据记录。这也是为什么B+树的叶结点包含了所有的关键字和对应的数据记录的指针，也是为什么B+树会有一个指针指向最左边的叶结点（B+树可以通过遍历所有叶结点来遍历所有的数据记录；但是由于B-树的叶结点全部为空，叶结点的父亲结点也不包括全部的关键字和对应的数据记录，无法通过遍历某一层的结点来遍历所有的数据记录）。

5.1 B-树的定义

一个m阶的B-树为满足下列条件的m叉树：

1. 每个分支节点最多有m棵子树；

2. 除根节点外，每个分支节点最少有⌈m/2⌉棵子树；

3. 根结点最少有两棵子树（除非根为叶结点，此时B-树只有一个结点）；

4. 所有“叶结点”都在同一层上，叶节点不包含任何关键字信息（可以把叶结点视为实际上不存在的外部结点，指向这些“叶结点”的指针为空）；

5. 所有分支结点中包含下列信息：

   n, p₀, key₁, p₁, key₂, p₁, ..., key_n, p_n

   其中n为结点中关键字值的个数，n≤m-1；

   key_i为关键字，且满足key_i<key_i+1，1≤i<n；

   p_i为指向该结点的第i+1棵子树的根的指针，0≤i≤n，p_i指的结点中所有关键字值都大于key_i。

5.2 B-树的查找

1. 分析：首先将给定的关键字k在B-树的根结点的关键字集合中采用顺序查找法或者折半查找法进行查找，若有k=key_i，则查找成功，根据相应的指针取得记录。否则，若k<keyi,则在指针p_i-1所指的结点中重复上述查找过程，直到在某结点中查找成功，或者有p_i-1=NULL，查找失败。

2. 算法

#define M 1000
typedef struct node {
	int keynum;
	keytype key[M+1];
	struct node *ptr[M+1];		// 自引用的指针
	rectype *recptr[M+1];		// 关键字对应的存储地址，指向key对应的数据记录，这些数据记录可能存储在磁盘上，也可能存储在内存中，取决于具体的B树实现和应用程序
} BNode;

keytype searchBTree(BNode *t,keytype k){
    int i, n;
    BNode *p = t;
    while(p!=NULL){
        n = p->keynum;		// 一共有n个
        p->key[n+1] = Maxkey;
        i = 1;
        while(k > p->key[i])	// 直到找到第一个≤k的key
        	i++;
        if(p->key[i] == k)
        	return p->key[i];
        else
        	p = p->ptr[i-1];           
    }
    return -1;
}

5.3 B-树的插入

1. 基本思想

   若将k插入到某结点后使得该结点中关键字值数目超过m-1时，则要以该结点位置居中的那个关键字值为界将该结点一分为二，产生一个新结点，并把位置居中的那个关键字值插入到双亲结点中；如双亲结点也出现上述情况，则需要再次进行分裂。最坏情况下，需要一直分裂到根结点，以致于使得B-树的深度加1。

2. 例

   

5.4 B+树的定义

一个m阶的B+树为满足下列条件的m叉树：

1. 每个分支结点最多有m棵子树；

2. 除根结点外，每个分支结点最少有⌈m/2⌉棵子树；

3. 根结点最少有两棵子树(除非根为叶结点结点,此时B+树只有一个结点)；

4. 具有n棵子树的结点中一定有n个关键字；

5. 叶结点中存放记录的关键字以及指向记录的指针，或者数据分块后每块的最大关键字值及指向该块的指针，并且叶结点按关键字值的大小顺序链接成线性链表。 key₁ p₁ key₂ p₂ …… key_n p_n

6. 所有分支结点可以看成是索引的索引，结点中仅包含它的各个孩子结点中最大(或最小)关键字值和指向孩子结点的指针。

   

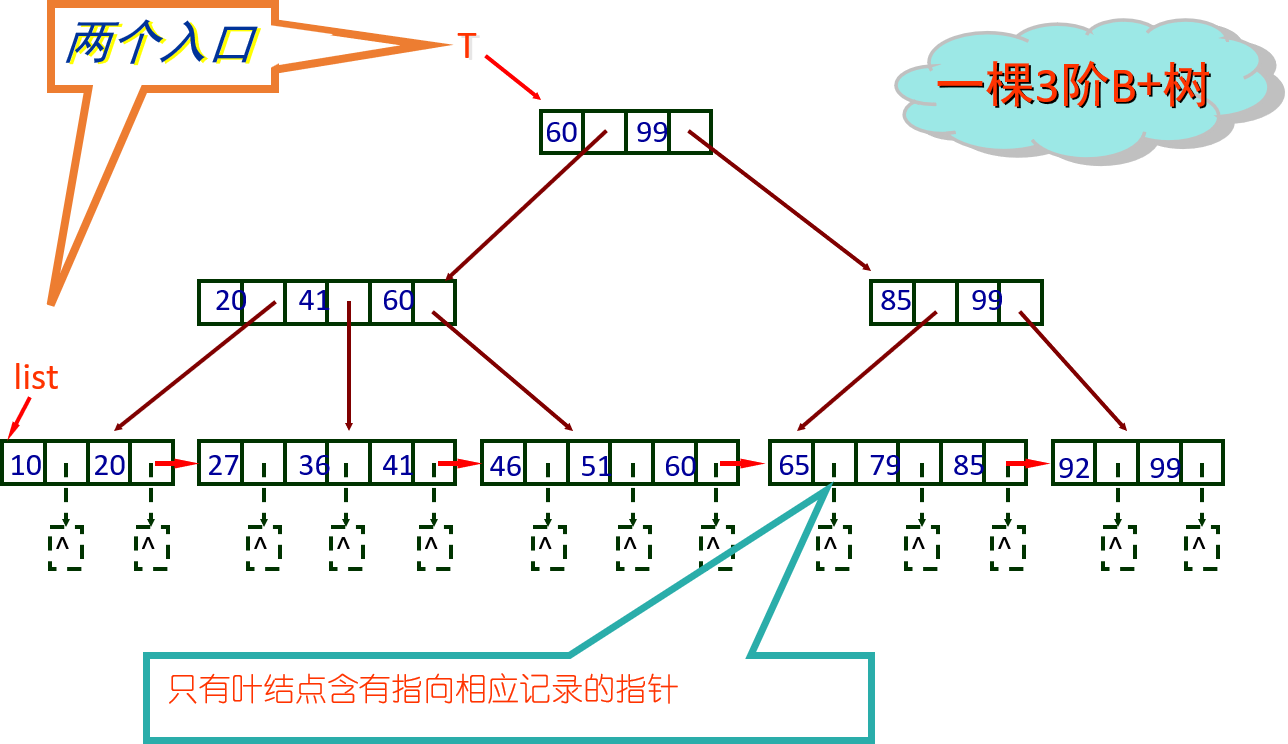
5.5 B-树和B+树的区别

1. B-树的每个分支结点中含有该结点中关键字值的个数，B+树没有；
2. B-树的每个分支结点中含有指向关键字值对应记录的指针，而B+树只有叶结点有指向关键字值对应记录的指针；
3. B-树只有一个指向根结点的入口，而B+树的叶结点被链接成为一个不等长的链表，因此，B+树有两个入口，一个指向根结点，另一个指向最左边的叶结点(即最小关键字所在的叶结点)。

6 散列(Hash)查找

6.1 三列查找的基本概念

1. A = H(k)

   其中k为记录的关键字，H(k)称为散列函数，或哈希(Hash)函数，或杂凑函数。函数值A为k对应的记录在查找表中的位置

2. 散列冲突

   对于不同的关键字k_i与k_j，经过散列得到相同的散列地址，即有H(k_i) = H(k_j)，这种现象称为散列冲突。

3. 什么是散列表

   根据构造的散列函数与处理冲突的方法将一组关键字映射到一个有限的连续地址集合上，并以关键字在该集合中的“象”作为记录的存储位置，按照这种方法组织起来表称为散列表，或哈希表，或称杂凑表；建立表的过程称为哈希造表或者散列，得到的存储位置称为散列地址或者杂凑地址。

6.2 散列函数的构造

1. 原则

   • 散列函数的定义域必须包括将要存储的全部关键字；若散列表允许有m个位置时，则函数的值域为[0 .. m–1](地址空间)。
   • 利用散列函数计算出来的地址应能尽可能均匀分布在整个地址空间中。
   • 散列函数应该尽可能简单，应该在较短的时间内计算出结果。

2. 确立散列表的步骤

   • 确定散列的地址空间(地址范围)；
   • 构造合适的散列函数；
   • 选择处理冲突的方法。

3. 散列函数的构造方法

   • 直接定址法

     一般形式：H(k) = ak + b

   • 数字分析法

   • 平方取中法

   • 叠加法

   • 除留余数法

     H(k) = k % p，其中，若m（散列地址为[0...m-1]）为地址范围大小（或称表长），则p可为小于等于m的素数

6.3 冲突的处理方法

所谓处理冲突，是在发生冲突时，为冲突的元素找到另一个散列地址以存放该元素。如果找到的地址仍然发生冲突，则继续为发生冲突的这个元素寻找另一个地址，直到不再发生冲突。

1. 开放地址法（闭散列方法）

   所谓开放地址法是在散列表中的“空”地址向处理冲突开放。即当散列表未满时，处理冲突需要的“下一个”地址在该散列表中解决。

   D_i = (H(k) + d_i) % m (i = 1, 2, 3, ...)

   其中，H(k)为哈希函数，m为表长，d_i为地址增量，有：

   1. d_i = 1, 2, 3, …, m–1 称为线性探测再散列
   2. d_i = 1², -1², 2², -2², …, 称为二次探测再散列
   3. d_i = 伪随机数序列 称为伪随机再散列

   聚集：散列地址不同的元素争夺同一个后继散列地址的现象

   • 产生聚集的主要原因：散列函数选择的不合适；负载因子过大

   • 负载因子(α)：衡量散列表的饱满程度 \[ \alpha = \frac{散列表中实际存入的元素数}{散列表中基本区的最大容量} \]

   特点：

   • “线性探测法”容易产生元素“聚集”的问题。
   • “二次探测法”可以较好地避免元素“聚集”的问题，但不能探测到表中的所有元素(至少可以探测到表中的一半元素)。
   • 只能对表项进行逻辑删除(如做删除标记)，而不能进行物理删除。使得表面上看起来很满的散列表实际上存在许多未用位置。

2. 再散列法

   D_i = H_i(k), i=1,2,3,...

   其中，D_i为散列地址，H_i(k)为不同的散列函数。

3. 链地址法

   将所有散列地址相同的记录链接成一个线性链表。若散列范围为[0...m-1]，则定义指针数组bucket[0...m-1]分别存放m个链表的头指针。

   

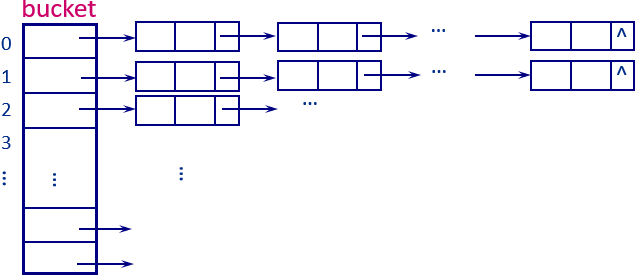
   散列表查找与创建的算法实现：

struct node{   
    ElemType data;
    struct node *next;
}; //list 
struct node *Hashtab[NHASH];

// 散列表的查找和创建函数：
// lookup: find key in Hashtab
struct node *lookup(ElemType key, int create){		// create为1则创建，否则只查找
    unsigned int h;
    strcut node *p;
    h = hash(key);		// h为key的hash函数值
    for(p=Hashtab[h]; p!=NULL; p=p->next)		// 遍历hash函数值为h的所有自变量
    if(p->data == key)
    	return p;
    if(create){		// create = 1
        p = (struct node *)malloc(sizeof(struct node));
        p->data = key; p->next = Hashtab[h];  Hashtab[h] = p;
	}
	return p;
}
// 当散列出现冲突时，新插入的元素放在链表的头部，这样算法简洁，效率更高；
// 由于链表查找效率低，可使用一棵二叉查找树或另一个散列表来代替链表解决冲突。

特点：

• 处理冲突简单，不会产生元素“聚集”现象，平均查找长度较小。
• 适合建立散列表之前难以确定表长的情况。
• 建立的散列表中进行删除操作简单。
• 由于指针域需占用额外空间，当规模较小时，不如“开放地址法”节省空间。

6.4 散列表的典型应用

1. 符号表

   散列表的一个典型应用是符号表（symbol），用于在数据值和动态符号（如变量名，关键码）集的成员间建立一种关联。符号表是编译系统中主要的数据结构，用于管理用户程序中各个变量的信息，通常编程系统使用散列表来组织符号表。散列表的思想就是把关键码送给一个散列函数，以产生一个散列值，这种值通常平均分布在一个适当的整数区间中，用作存储信息的表的下标。常见做法是为每一个散列值关联一个数据项的链表，这此项共有同一个散列值（散列冲突）。

   符号表的定义使用：

struct val{ //符号散列表义：
    char *name;
    int value;
    struct val *next;
};
struct val *symtab[NHASH];

// 符号查找和创建函数：
// lookup: find name in symtab
struct val *lookup(char *name, int create){
	int h;
    strcut val *p;
    h = hash(name);
    for(p=symtab[h]; p!=NULL; p=p->next)
        if(strcmp(name, p->name) == 0)
            return p;
    if(create){
        p = (struct val *)malloc(sizeof(struct val));
        p->name = name; p->next = symtab[h];  symtab[h] = p;
    }
    return p;
}

// Hash函数：
// hash: compute hash value of string
enum{ 
    MULTIPLIER = 31
}; //根据经验，对于ASCII串31,37很好

unsigned int hash(char *str){
    unsigned int h=0; 
    char *s;
    for(s=str; *s!='\0'; s++)
        h = MULTIPLIER * h + *s;
    return h%NHASH;
}

2. 一个针对字符串好的Hash函数：

// ( from Data Structures and Algorithm Analysis in C – Mark Allen Weiss)
// hash: compute hash value of string
unsigned int hash(char *str){
    unsigned int h=0;
    while(*str != '\0')
        h = (h<<5) + *str++;
    return h%TableSize;
}

6.5 例：词频统计——Hash表

1. 问题：编写程序统计一个文件中每个单词的出现次数（词频统计），并按字典序输出每个单词及出现次数。

2. 算法分析：基本上只有查找和插入操作。

   

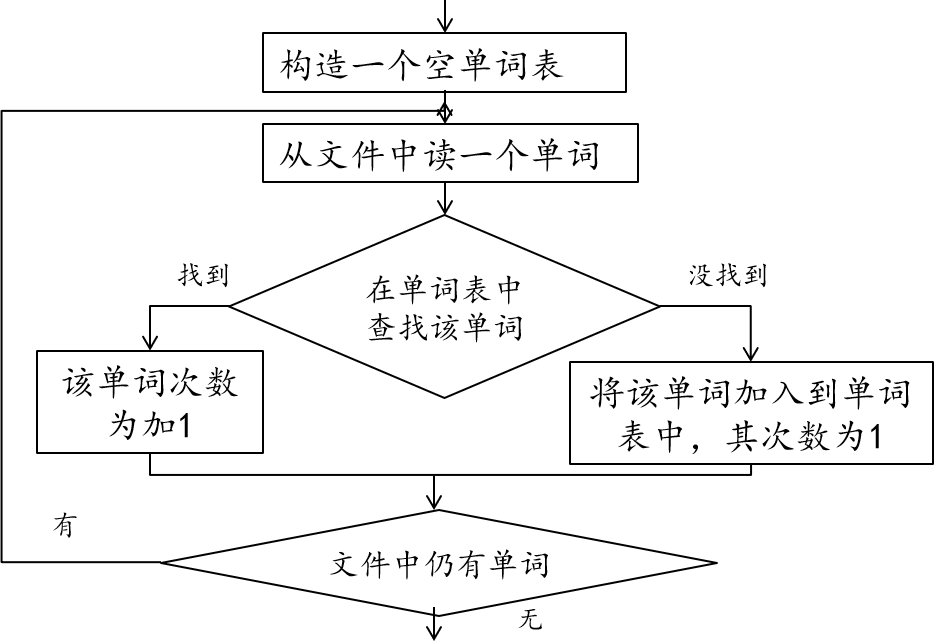
   本问题有如下特点：

   1. 问题规模不知（即需要统计的单词数量末知），有可很大，如对一本小说进行词频统计；

   2. 单词表在查找时需要频繁的执行插入操作，是一种典型的动态查找表。

   针对上述问题，在“线性表”一章采用了顺序表、链表来实现；在“树”一章中采用了二叉排序树（BST）来实现。BST实现方式虽然查找效率较高，但由于树并不是理想的平衡树，查找效率不如折半查找。有没有更好的方法提高查找效率？