【数据结构】ds笔记4-栈和队

说在前面

本篇笔记总结DSPv2b_4(栈与队) for student内的相关内容。各位如果在学习过程中对于一些概念不理解，可以考虑问问AI们，从他们那里获得一些形象的描述来辅助理解。以及，如果实在de不出来bug了，也可以问问AI，虽然不一定有用，但是万一有什么bug被你忽略缺被AI发现了呢。最后，本人学艺不精，只是一边看着ppt一边敲敲改改，如有疏漏，欢迎提出喵~o( =∩ω∩= )m

栈

1 栈的基本概念

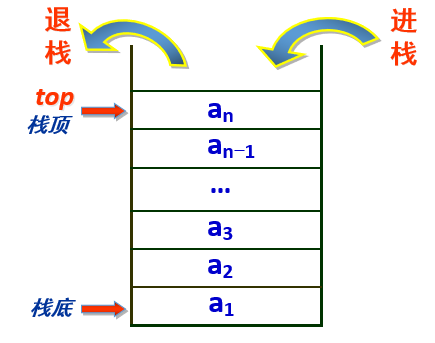
1.1 栈的定义

  • 栈（Stack）是一种只允许在表的一端进行插入操作和删除操作的线性表。允许操作的一端称为顶，栈顶元素的位置由一个称为栈顶位置的变量给出。当表中没有元素时，称之为空栈。

  • 栈的特点

    • 元素间呈线性关系
    • 插入删除在一端进行
    • 后进先出(LIFO(Last-In-First-Out))

1.2 栈的基本操作

  • 特殊性：

    • 其操作仅仅是一般线性表的操作的一个子集

    • 插入和删除操作的位置受到限制

  • 基本操作：

    • 插入（进栈、入栈、压栈）
    • 删除（出栈、退栈、弹出）
    • 测试栈是否为空
    • 测试栈是否已满
    • 获取栈顶元素

2 栈的顺序存储结构（顺序栈）

2.1 构造原理

  • 利用一维数组STACK[0...M–1]来表示,同时定义一个整型变量(top)给出栈顶元素的位置。

  • 溢出

    • 上溢(top = M-1)：栈已满时做入栈操作
    • 下溢(top = -1)：栈为空时作出栈操作

  • 类型定义

    1
    2
    3
    4
    #define MAXSIZE 1000
    ElemType STACK[MAXSIZE];
    int Top = -1;
    // 由于Top变量需要在多个函数间共享，为了保持函数接口简洁，在此定义为全局变量

2.2 基本算法

2.2.1 初始化堆栈

1
2
3
void initStack( ){
	Top= –1;
}

2.2.2 进栈

1
2
3
4
5
6
7
8
9
10
11
void push(ElemType s[ ], ElmeType item ){
	if(isFull())
		Error("Full Stack!");
	else
		s[++Top] = item;	// 入栈成功
}

void Error(char s[]){
	printf("%s\n", s);
	exit(-1);
}

2.2.3 出栈

1
2
3
4
5
6
ElemType pop(ElemType s[ ]){
	if(isEmpty())
		Error("Empty Stack!");
	else
		return s[Top--];	// 出栈成功
}

2.2.4 测试栈是否为空

1
2
3
int isEmpty( ){		// 栈空，返回1；否则，返回0
	return Top == -1;
}

2.2.5 测试栈是否已满

1
2
3
int isFull( ){		// 栈满,返回1；否则,返回0。
	return Top == MAXSIZE-1;
}

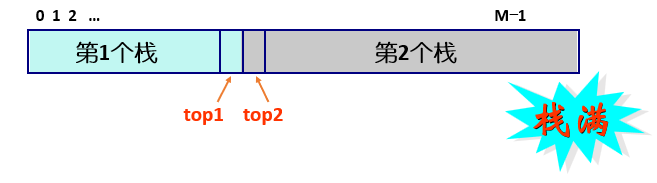
2.3 多栈共享连续空间问题——以两个栈共享一个数组为例

已知数组STACK[0...M-1]、第一个与第二个栈的栈顶元素的位置Top1, Top2

2.3.1 进栈

1
2
3
4
5
6
7
8
9
10
11
12
// 规则：当i=1时，将item插入第1个栈；当i=2时，将item插入第2个栈。
void push(ElemType s[ ], int i, ElemType item){
    if(top1==top2–1){				// 栈满
    	Error("Full Stack!");
    }else{ 
        if(i==1)                    // 插入第1个栈
        	STACK[++top1]=item;
        else						// 插入第2个栈
        	STACK[--top2]=item;
        return;
    }
}

2.3.2 出栈

1
2
3
4
5
6
7
8
9
10
11
12
13
14
// 规则：当i=1时，删除第1个栈的栈顶元素；当i=2时，删除第二个栈的栈顶元素
EleType pop(ElemType s[ ], int i){
    if(i==1){	// 对第一个栈做操作
        if(top1==–1) 
        	Error("Empty Stack1!");
    	else   
    		return s[top1--];
    }else{		// 对第二个栈做操作
    	if(top2==MAXSIZE)
    		Error("Empty Stack2!"); 
    	else
    		return s[top2++];
    }
}

3 栈的链式存储结构（链接栈）（链栈）

3.1 构造原理

  • 用一个线性链表来实现一个栈结构, 同时设置一个指针变量(top)指出当前栈顶元素所在链结点的位置。栈为空时，有top=NULL。

  • 链栈是一种特殊的链表，其结点的插入（进栈）和删除（出栈）操作始终在链表的头。

  • 类型定义

    1
    2
    3
    4
    5
    6
    7
    struct node{ 
        ElmeType data;
        struct node *link;
    };
    typedef struct node *Nodeptr;
    typedef struct node Node;
    Nodeptr Top;		//即为链表的头结点指针

3.2 基本算法

3.2.1 初始化堆栈

1
2
3
void initStack( ){
	Top=NULL;
}

3.2.2 进栈

1
2
3
4
5
6
7
8
9
10
11
// 等效于在链表前面插入一个新结点
void push(ElemType item){
    Nodeptr p;
    if( (p=(Nodeptr)malloc(sizeof(Node)))==NULL ){
    	Error("No memory!");  
    }else{
        p->data=item;		// 将item送新结点数据域
        p->link=Top;		// 将新结点插在链表最前面
        Top=p;				// 修改栈顶指针的指向
    }
}

3.2.3 出栈

1
2
3
4
5
6
7
8
9
10
11
12
13
ElemType pop( ){
	Nodeptr p;
    ElemType item;
    if(isEmpty( )){ 
    	Error("Empty Stack!");		// 栈中无元素
    }else{
        p=Top;		// 暂时保存栈顶结点的地址
        item=Top->data;		// 保存被删栈顶的数据信息
        Top=Top->link;		// 删除栈顶结点
        free(p);			// 释放被删除结点
        return item;		// 返回出栈元素
    }
}

3.2.4 测试栈是否为空

1
2
3
int isEmpty( ){
	return Top==NULL;
}

4 例题：计算器（表达式计算）

4.1 提出问题

  • 问题描述：从标准输入中读入一个整数算术运算表达式，如24 / ( 1 + 2 + 36 / 6 / 2 - 2) * ( 12 / 2 / 2 )=，计算表达式结果，并输出。

    要求：

    • 表达式运算符只有+、-、*、/，表达式末尾的=字符表示表达式输入结束，表达式中可能会出现空格；
    • 表达式中会出现圆括号，括号可能嵌套，不会出现错误的表达式；
    • 出现除号/时，以整数相除进行运算，结果仍为整数，例如：5/3结果应为1。

  • 输入形式：从键盘输入一个以=结尾的整数算术运算表达式。

  • 输出形式：在屏幕上输出计算结果（为整数）。

  • 样例输入：24 / ( 1 + 2 + 36 / 6 / 2 - 2) * ( 12 / 2 / 2 )=

  • 样例输出：18

4.2 问题分析

  • 中缀表达式(infix)

    对于一般形式的表达式通常称为中缀表达式，如a+b*c + (d*e+f)/g

    计算机计算表达式的值时面临如下问题：运算符有优先级、括号会改变计算的次序

  • 后缀表达式(Postfix)

    最大好处是没有括号且不用考虑运算符的优先级

  • 中缀到后缀的转换规则

    从左至右遍历中缀表达式中每个数字和符号：

    • 若是数字直接输出，即成为后缀表达式的一部分；

    • 若是符号：

      • 若是)，则将栈中元素弹出并输出，直到遇到(,(弹出但不输出；

      • 若是(,+,*等符号，则从栈中弹出并输出优先级高于当前的符号，直到遇到一个优先级低的符号；然后将当前符号压入栈中。

        （优先级+,-最低,*,/次之,(最高）

      • 遍历结束，将栈中所有元素依次弹出，直到栈为空。

  • 后缀表达式计算

    从左至右遍历后缀表达式中每个数字和符号：

    • 若是数字直接进栈；
    • 若是运算符（+,-,*,/），则从栈中弹出两个元素进行计算（注意：后弹出的是左运算数），并将计算结果进栈。
    • 遍历结束，将计算结果从栈中弹出（栈中应只有一个元素，否则表达式有错）。

4.3 算法设计

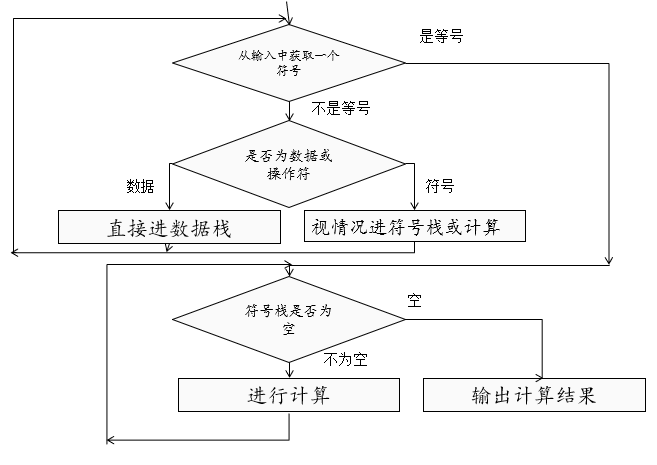
对于问题3.1我们没有必要象编译程序那样先将中缀表达式转换为后缀表达式，然后再进行计算。我们可以设两个栈，一个为数据栈，另一个为运算符栈，在转换中缀表达式的同时进行表达式的计算。主要思路为：当一个运算符出栈时，即与数据栈中的数据进行相应计算，计算结果仍存至数据栈中。算法如下：

从输入（中缀表达式）中获取一项：

  • 若是数字则压入数据栈中；
  • 若是符号：
    • 若是)，则将符号栈中元素弹出并与数据栈中元素进行计算、计算结果放回数据栈中，直到遇到(， (弹出但不计算；
    • 若是(，+，*等符号，则从符号栈中弹出优先级高于当前的符号并与数据栈中元素进行计算、计算结果放回数据栈中，直到遇到一个优先级低的符号；然后将当前符号压入栈中。
    • 若是=号，将符号栈中所有元素依次弹出并与数据栈中元素进行计算、计算结果放回数据栈中，直到符号栈为空，此时数据栈中为计算结果；否则继续从输入中获取一项。

4.4 代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<ctype.h>
#define MAXSIZE 100
typedef  int  DataType;  //可以方便扩展为浮点型
enum symbol {NUM, OP, EQ, OTHER};//符号类型
enum oper {EPT, ADD, MIN, MUL, DIV, LEFT, RIGHT}; //运算符，把括号和等号视为运算符
int Pri[]={-1,0,0,1,1,2,2}; //运算符优先级
union sym {
    DataType num;
    enum oper op;
} ; //符号有两类：运算数和运算符
DataType Num_stack[MAXSIZE]; //数据栈
enum oper Op_stack[MAXSIZE]; //符号栈
int Ntop=-1; //数据栈顶指示器，初始为空栈
int Otop=-1; //运算符栈顶指示器，初始为空栈
enum symbol getSym( union sym *item);
void operate(enum oper op );//操作运算符
void compute(enum oper op ); //进行运算
void pushNum(DataType num);
DataType popNum();
void pushOp(enum oper op);
enum oper popOp();
enum oper topOp();

int main(){
    union sym item;
    enum symbol s;
    //下面读入等号前的运算数和运算符
    while( (s = getSym(&item)) != EQ){
        if(s == NUM){       // 运算数进数据栈
            pushNum(item.num);
        }else if(s == OP){      // 对运算符分情况分别处理
            operate(item.op);
        }else{      // 不是运算符、运算数和等号，输入有问题
            printf("Error in the expression!\n");
            return 1;
        }
    }
    // 下面是读入了等号
    while(Otop >= 0)    //将栈中所有运算符弹出计算
        compute(popOp());
    if(Ntop == 0)  //正常情况下，运算符栈为空，数据栈有一个数据
        printf("%d\n", popNum());   // 数据栈只有一个最后结果
    else    // 不然就是输入出问题啦
        printf("Error in the expression!\n");
    return 0;
}

enum symbol getSym( union sym *item){
    int c, n;
    while((c = getchar()) != '=') {
        if(c >= '0' && c <= '9'){
            for(n=0; c >= '0' && c <= '9'; c= getchar())
            n = n*10 + c-'0';
            ungetc(c, stdin);   //回退到缓冲区
            item->num = n;
            return NUM;
        }else {
            switch (c) {
                case '+':item->op = ADD;return OP;
                case '-':item->op = MIN;return OP;
                case '*':item->op = MUL;return OP;
                case '/':item->op = DIV;return OP;
                case '(':item->op = LEFT;return OP;
                case ')':item->op = RIGHT;return OP;
                case ' ':case '\t':case '\n':break;
                default:return OTHER;
            }
        }
    }
    return EQ;
}

void operate(enum oper op){
    enum oper t;
    if(op != RIGHT){  // 不是右括号
        while(Pri[op] <= Pri[topOp()] && topOp() != LEFT)
            compute(popOp()); //栈顶不是左括号且优先级大于等
        pushOp(op);
    }
    else    // 读入的是右括号
        while((t = popOp()) != LEFT)    // 出栈的是左括号无操作
            compute(t);   //读入是右括号时栈中左括号前的都计算掉
}

void compute(enum oper op ){
    DataType tmp;
    switch(op) {
        case ADD:
            pushNum(popNum() + popNum()); break;
        case MIN:
            tmp = popNum();//先出栈的是右运算数
            pushNum(popNum() - tmp); break;
        case  MUL:
            pushNum(popNum() * popNum()); break;
        case DIV:
            tmp = popNum();     // 后出栈的是左运算数
            pushNum(popNum() / tmp); break;
    }
}

//数据栈操作
void pushNum(DataType num){
    if(Ntop == MAXSIZE -1){
        printf("Data stack is full!\n");
        exit(1);
    }
    Num_stack[++Ntop] = num;
}

DataType popNum(){
    if(Ntop == -1) {
        printf("Error in the expression!\n");
        exit(1);
    }
    return Num_stack[Ntop--] ;
}

// 运算符栈操作
void pushOp(enum oper op){
    if(Ntop == MAXSIZE -1) {
        printf("operator stack is full!\n");
        exit(1);
    }
    Op_stack[++Otop] = op;
}

enum oper popOp(){
    if(Otop != -1){
        return Op_stack[Otop--] ;
    }
    return EPT;
}

enum oper topOp(){
    return Op_stack[Otop];
}

队

1 队的基本概念

1.1 队的定义

队列简称队。是一种只允许在表的一端进行插入操作，而在表的另一端进行删除操作的线性表（先进先出 FIFO(First-In-First-Out)）。允许插入的一端称为队尾，队尾元素的位置由rear指出；允许删除的一端称为队头, 队头元素的位置由front指出。

### 1.2 队的基本操作

  1. 特殊性
    1. 其操作仅是一般线性表的操作的一个子集
    2. 插入和删除操作的位置受到限制
  2. 队的基本操作
    1. 插入（进队、入队）
    2. 删除（出队、退队）
    3. 测试队是否为空
    4. 测试队是否为满
    5. 检索当前队头元素
    6. 创建一个空队

2 队的顺序存储结构

2.1 构造原理

借助一个一维数组QUEUE[0...M–1]来描述队的顺序存储结构，同时，设置两个变量front与rear分别指出当前队头元素与队尾元素的位置，再设置变量count指出实际队中元素个数。

初始时队为空，front = 0, rear = -1, count = 0；测试队为空的条件为count == 0

2.2 循环队列

  • 把队列(数组)设想成头尾相连的循环表，使得数组前部由于删除操作而导致的无用空间尽可能得到重复利用，这样的队列称为循环队列。

  • 类型定义

    1
    2
    3
    #define MAXSIZE 1000
    ElemType QUEUE[MAXSIZE];
    int Front, Rear, Count;

2.3（循环队列）基本算法

2.3.1 初始化队列

1
2
3
4
5
void initQueue( ) {
    Front = 0;
    Rear = MAXSIZE-1;
    Count = 0;
}

2.3.2 测试队列是否为空或满

1
2
3
4
5
6
7
int isEmpty( ){		// 队空，返回1；否则，返回0
	return Count == 0;
}

int isFull( ){
	return Count == MAXSIZE;
}

2.3.3 进队

1
2
3
4
5
6
7
8
9
void enQueue(ElemType queue[ ], ElemType item){
    if(isFull()){	// 队满，插入失败
    	Error(“Full queue!”);
    }else{		// 队未满，插入成功
        Rear = (Rear+1) % MAXSIZE; 
        queue[Rear]=item;
        Count++;
    }
 }

2.3.3 出队

1
2
3
4
5
6
7
8
9
10
11
ElemType deQueue(ElemType queue[ ]){ 
    ElemType e;
    if(isEmpty()){
    	Error(“Empty queue!”);		// 队空，删除失败
    }else{
        e=queue[Front];
        Count--;		// 队非空，删除成功
        Front = (Front+1)%MAXSIZE;
        return e;
    }
}

3 队的链式存储结构

3.1 构造原理

  • 队列的链式存储结构是用一个线性链表表示一个队列，指针front与rear分别指向实际队头元素与实际队尾元素所在的链结点。

  • 类型定义

    1
    2
    3
    4
    5
    6
    7
    struct node{ 
        ElmeType data;
        struct node *link;
    }
    typedef struct node QNode;
    typedef struct node *QNodeptr;
    QNodeptr Front, Rear;

3.2 基本算法

3.2.1 初始化队列

1
2
3
4
void initQueue(){
    Front=NULL;
    Rear=NULL；
}

3.2.2 测试队列是否为空

1
2
3
int isEmpty(){		// 队空，返回1；否则，返回0
	return Front==NULL;
}

3.2.3 进队

1
2
3
4
5
6
7
8
9
10
11
12
void enLQueue(ElemType data){     
    QNodeptr p;
    if((p=(QNodeptr)malloc(sizeof(QNode))) ==NULL)  /* 申请链结点 */
    	Error("No memory!");
    p->data = data;
    p->link = NULL;
    if(Front == NULL) 	// 插入空队的情况
    	Front = p;
    else
        Rear->link = p;	// 插入非空队的情况 
    Rear=p;
}

3.2.4 出队

1
2
3
4
5
6
7
8
9
10
11
12
13
ElemType deLQueue( ){
    QNodeptr p;
    ElemType data;
    if(isEmpty()){		// 队为空，删除失败
    	Error("Empty queue!");
    }else{				// 队非空，删除成功
        p = Front;
        Front = Front->link;
        data = p->data;
        free(p);     
        return data;
    }
}

3.2.5 销毁一个队

所谓销毁一个队是指将队列所对应的链表中所有结点都删除，并且释放其存储空间，使队成为一个空队(空链表)。

1
2
3
4
5
6
7
void destroyLQueue(){
    while(Front != NULL){                    /* 队非空时  */
        Rear=Front->link;    
        free(Front);                 /* 释放一个结点空间  */
        Front=Rear;
    }
}

4 例题：银行排队模拟

4.1 提出问题

  • 某银行网点有五个服务窗口，分别为三个对私、一个对公和一个外币窗口。通常对私业务人很多，其它窗口人则较少，可临时改为对私服务。假设当对私窗口客户平均排队人数超过7人时，客户将有抱怨，此时银行可临时将其它窗口中一个或两个改为对私服务，当客户少于7人时，将恢复原有业务。设计一个程序用来模拟银行服务。

  • 输入：首先输入一个整数表示时间周期数，然后再依次输入每个时间周期中因私业务的到达 客户数。注：一个时间周期指的是银行处理一笔业务的平均处理时间，可以是一分钟、三分钟或其它。例如：

    6

    2 5 13 11 15 9

    说明：表明在6个时间周期内，第1个周期来了2个（ID分别为1,2），第2个来了5人（ID分别为3,4,5,6,7），以此类推。

  • 输出：每个客户等待服务的时间周期数。

4.2 问题分析

在生产者-消费者应用中消费者显然是先来先得到服务。在此，显然可用一个队列来存放等待服务的客户队列。每个客户有二个基本属性：排队序号和等待时间（时间周期数）：

1
2
3
4
5
struct cust {
    int id;			//客户排队序号
    int wtime;		//客户等待服务的时间（时间周期数）
};
struct cust Cqueue[MAXSIZE]; //等待服务的客户队列，一个循环队列

为了简化问题，可用一个变量来表示银行当前提供服务的窗口数：int snum;在本问题中，该变量的取值范围为3<=snum<= 5

4.3 算法设计

1
2
3
4
5
6
7
8
9
10
11
12
13
主要算法：
for(clock=1; ; clock++){	//在每个时间周期内
{
	if(客户等待队列非空)
		将每个客户的等待时间增加一个时间单元；
	if(clock <= simulationtime)
		如果有新客户到来（从输入中读入本周期内新来客户数），将其入队；
		根据等待服务客户数重新计算服务窗口数；
	if(客户等待队列非空)
		从客户队列中取（出队）相应数目（按实际服务窗口数）客户获得服务；
		然后根据等待服务客户数重新计算服务窗口数；
	else 结束模拟
}

4.4 代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
#include <stdio.h>
#include  <stdlib.h>
#define  MAXSIZE 200  //队列容量
#define THRESHOLD  7  //窗口增加阈值
#define MAXSVR  5   //最大服务窗口数
#define MINSVR  3    //最小服务窗口数
typedef struct {
    int id;
    int wtime;
} CustType;
int Winnum=MINSVR; //提供服务的窗口数
void updateCustqueue(); //更新等待队列中客户等待时间
void enCustqueue(CustType c); //客户入等待队列
CustType deCustqueue(); //客户出队
int getCustnum();   //获取队中等待客户人数
int isFull();
int isEmpty();
void arriveCust(); //获取新客户，并加至等待队列中
int service(); //银行从队列中获取客户进行服务

#define  MAXSIZE 200  //队列容量
static CustType Cqueue[MAXSIZE];//客户等待队列
static int Cfront=0; //队头队尾指示器
static int Crear = -1;   //队尾
static int Cnum=0;      // 队中元素个数

int main(){
    int clock, simulationtime;
    scanf("%d", &simulationtime);
    for(clock = 1; ; clock++){
        updateCustqueue();
        if(clock <= simulationtime)
            arriveCust();
        if(service()==0 && clock>simulationtime)
            break;      // 等待队列为空且不会有新客户
    }
    return 0;
}

void arriveCust(){
    int i,n;
    static int count=1;
    CustType c;
    scanf("%d", &n);
    for(i=0; i<n; i++){
        c.id = count++; c.wtime = 0;
        enCustqueue(c);
    }
    while((getCustnum() / Winnum) >= THRESHOLD && Winnum<MAXSVR)  //增加服务窗口
        Winnum++;
}

int service(){
    int i;
    CustType c;
    for(i=0; i<Winnum; i++)
        if(isEmpty()){
            return 0;
        }else {
            c = deCustqueue();
            printf("%d :%d\n", c.id, c.wtime);
        }
    if((getCustnum() / Winnum) < THRESHOLD && Winnum>MINSVR)
        Winnum--;
    return 1;
}

void enCustqueue(CustType c){
    if(isFull()){   // 队满，插入失败
        printf("Full queue!");
        exit(-1);
    }else{      // 队未满，插入成功
        Crear = (Crear+1) % MAXSIZE;
        Cqueue[Crear] = c;
        Cnum++;
    }
}

CustType deCustqueue(){
    CustType c;
    if(isEmpty()){
        printf("Empty queue!");
        exit(-1);
    }else{
        c=Cqueue[Cfront];       // 队非空，删除成功
        Cnum--;
        Cfront = (Cfront+1)%MAXSIZE;
        return c;
    }
}

void updateCustqueue(){
    int i;
    for(i=0; i<Cnum; i++)
        Cqueue[(Cfront+i)%MAXSIZE].wtime++;
}

int isEmpty(){
    return Cnum == 0;
}

int isFull(){
    return Cnum == MAXSIZE;
}

int getCustnum(){
    return Cnum;
}

其他

1 枚举类型(enum)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
// 1 定义形式：
	enum 枚举名 {值表}
	enum color {red, green, yellow, white, black}	// 枚举值是标识符
// 2 枚举变量说明
	enum color chair;
	enum color suite[10];
// 3 在表达式中使用枚举变量
	chair = red;
	suite[5] = yellow;
	if(chair == green)...
// 4 注意：对枚举变量的赋值并不是将标识符字符串传给它，而是把该标识符所对应的各值表中常数值赋与变量。C语言编译程序把值表中的标识符视为从0开始的连续整数。另外，枚举类型变量的作用范围与一般变量的定义相同。
	// 如：
		enum color { red, green, yellow = 5, white, black };
	// 则：
		red=0, green=1, yellow=5, white=6, black=7
// 5 枚举类型用途
    // 用来说明变量取值为有限的一组值之一，如：
    	enum Boolean { FALSE, TRUE };
	// 用来定义整型常量，如：
		enum { SIZE=1024 };
	// 符号类型变量可用于数组下标

2 静态变量(static)

  • 内部静态变量

    • 在局部变量前加上static关键字就成为内部静态变量。

    • 内部静态变量仍是局部变量，其作用域仍在定义它的函数内。但该变量采用静态存贮分配（在编译时分配空间），当函数执行完，返回调用点时，该变量的值将继续保留，下次再进入该函数时，其值仍存在。

      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      14
      15
      // 例：下列程序打印结果为：1 2 4 7 11
      #include <stdio.h>
      int f(int i);

      int main(){ 
          int i; 
          for(i=0; i < 5; i++) 
          	printf("%d ",f(i)); 
      }

      int f(int i){ 
      	static int k = 1; 
      	k += i; 
      	return (k); 
      }

  • 外部静态变量

    • 在函数外部定义的变量前加上static关键字便成了外部静态变量。
    • 作用域为定义它的文件，即成为该文件的的“私有”（private）变量，其它文件上的函数一律不得直接进行访问，除非通过它所在文件上的各种函数来对它进行操作，这可实现数据隐藏。(在C++中提供进一步的数据隐藏。)
学习经验 > 数据结构
#学习经验
【数据结构】ds笔记4-栈和队
http://example.com/2024/04/03/LE-ds4/
Author
John Doe
Posted on
April 3, 2024
Licensed under