【数据结构】ds笔记3-广义表、矩阵与串

说在前面

本篇笔记总结了DSPv2b_3(广义表、矩阵与串) for student内的相关内容，按照ppt上内容，笔记顺序为矩阵、广义表、串。不过据说本节内容“不考”，“不讲不学不考但是说不定什么时候就用到了”。最后，本人学艺不精，只是一边看着ppt一边敲敲改改，如有疏漏，欢迎提出喵~o( =∩ω∩= )m

1 矩阵

1.1 特殊矩阵的压缩存储

压缩存储：为多个值相同的元素, 或者位置分布有规律的元素分配尽可能少的存储空间，而对0元素一般情况下不分配存储空间。

目的：节省存储空间

1.1.1 对称矩阵的压缩存储

对称矩阵：满足a_ij=a_ji(1<=i,j<=n)的n阶矩阵

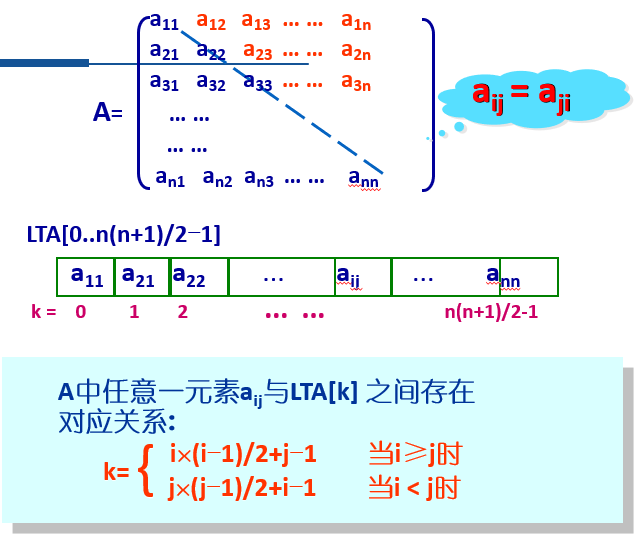
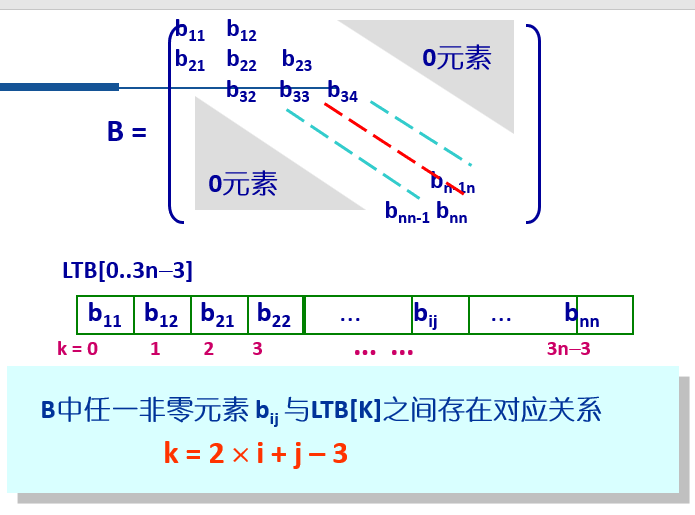
1.1.2 对角矩阵的压缩存储

对角矩阵：一个矩阵中，值非0的元素对称地集中在主对角线两旁的一个带状区域中(该区域之外的元素都为0元素)
例：三对角矩阵

1.2 稀疏矩阵的三元组表表示

稀疏矩阵：一个较大的矩阵中，零元素的个数相对于整个矩阵元素的总个数所占比例较大时，可以称该矩阵为一个稀疏矩阵。
三元组表示：(i, j, value)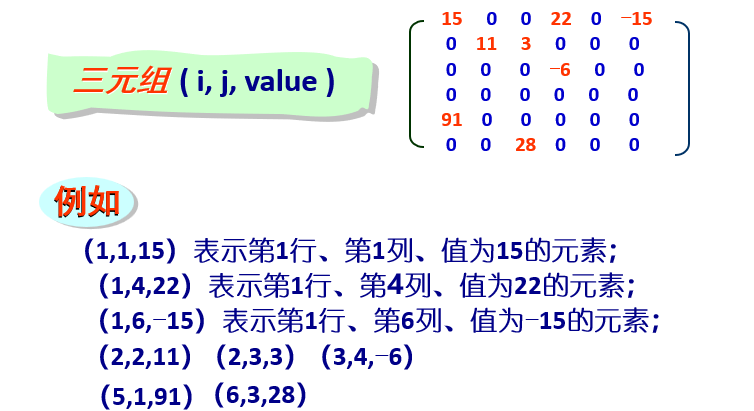
一个特殊的三元组：(m, n, t)
- 其中m表示矩阵总行数，n表示矩阵总列数，t表示非零元素总个数。
- 若一个mxn阶稀疏矩阵具有t个非零元素，则用t+1个三元组来存储,其中第一
  
  三元组分别用来给出稀疏矩阵的总行数m、总列数n以及非零元素的总个数t；第二个三元组到第t+1个三元组按行序为主序的方式依次存储t个非零元素。
- 例：
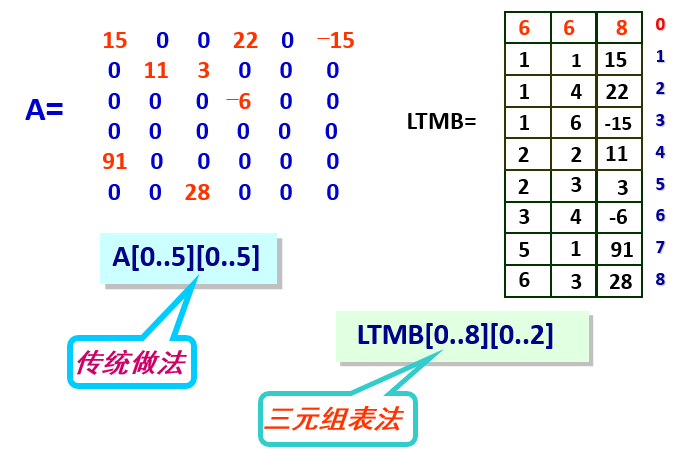
对于一个具有t个非零元素的mxn阶矩阵,若采用三元组表方法存储, 则当t<(mxn)/3-1,这样做才有意义。

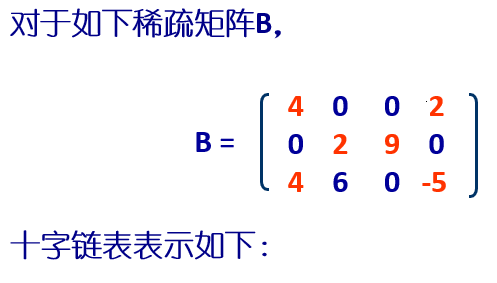
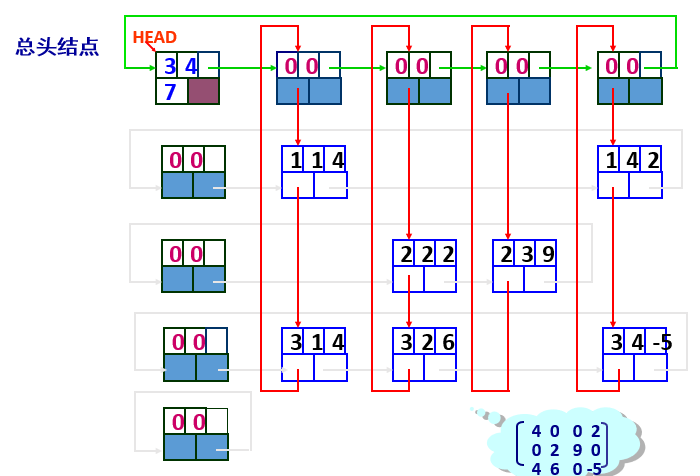
1.3 稀疏矩阵的十字链表表示

十字链表：为稀疏矩阵的每一行设置一个单独的循环链表，同样为每一列设置一个单独的循环链表。矩阵中每一个非零元素同时包含在两个循环链表中，即包含在它所在的行链表所在的列链表中, 即两个链表的交汇处。
普通链结点构造：

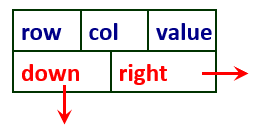
其中，row, col, value分别表示某个非零元素所在的行号、列号和元素的值；down和right分别为向下与向右指针，分别用来链接同一列中的与同一行中的所有非零元素对应的链结点。
行链表表头结点和列链表表头结点构造：

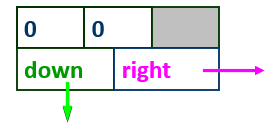
对m个行链表，分别设置个行链表表头结点。表头结点的构造与链表中其他链结点一样，只是令row与col的值分别为0，right域指向相应行链表的第一个结链点。

同理,对n个列链表，分别设置n个列链表表头结点指向相应列链表的第一个结链点。
总头结点构造：

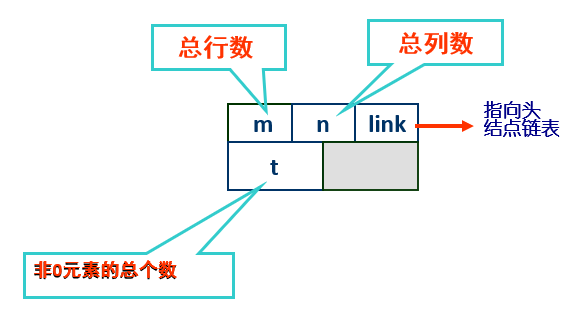
通过value也即link域把所有头结点也连接成一个循环链表
例：

1.4 例

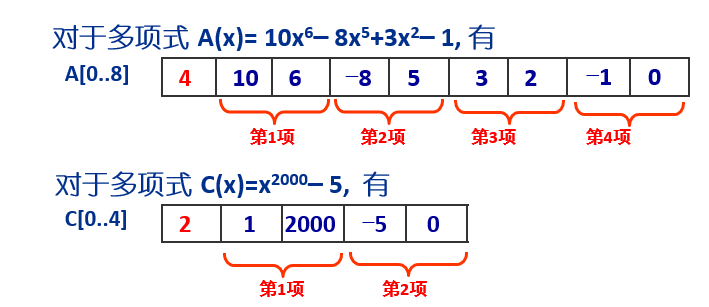
1.4.1 一元n阶多项式的数组表示

一个标准的一元n阶多项式的各项若按降幂排列，可以表示为如下形式:

A_n(x) = a_nxⁿ + a_n-1x^n-1 + ... + a₁x + a₀
方法一：一维数组

定义一个一维数组A[0...n+1]来存储多项式，其中，A[0]用来存放多项式的阶数n;A[1]~A[n+1]依次用来存放多项式的n+1项的系数。
方法2：压缩存储

定义一个一维数组A[0...2m]来存储多项式，其中，A[0]存放系数非零项的总项数m；A[1]~A[2m]依次存放系数非零项各项的系数与指数偶对(一共m个这样的偶对)。

1.4.2 n阶“魔方”（n为任意奇数）

题目：以3阶模仿为例，将1~9不重复地填在3行3列的9个方格中，分别使得每一行、每一列、两个对角线上的元素之和都等于15。
算法：
1. 将用做“魔方”的二维数组的所有元素清0；
2. 第一个数填在第一行居中的位置上(i=0，j=n/2)；
3. 3.以后每填一个数后，将位置移到当前位置(i,j)的左上角，即做动作i=i-1，j=j-1；
4. 根据不同情况对位置进行修正：
  1. 若位置(i,j)上已经填数，或者i,j同时小于0，将位置修改为i=i+2，j=j+1；
  2. 若i小于0，但j不小于0，修改i为n-1；
  3. 若j小于0，但i不小于0，修改j为n-1。

代码实现

void magic(int a[], int n){
    int  i, j, num;
    for(i=0; i<n; i++)
    	for(j=0; j<n; j++) 
    		a[i][j]=0;               /* 魔方清0 */
    i=0;
    j=n/2;                               /* 确定i与j的初始位置 */
    for(num=1; num<=n*n; num++){
        if(i<0 && j<0 || a[i][j]!=0){
            i+=2;
            j++;
        }
        a[i--][j--]=num;      /* 填数，并且左上移一个位置 */
        if(i<0 && j>=0)  
            i=n-1;                   /* 修正i的位置 */
        if(j<0 && i>=0)  
            j=n-1;                   /* 修正j的位置 */
    }
}

2 广义表

2.1 广义表的基本概念

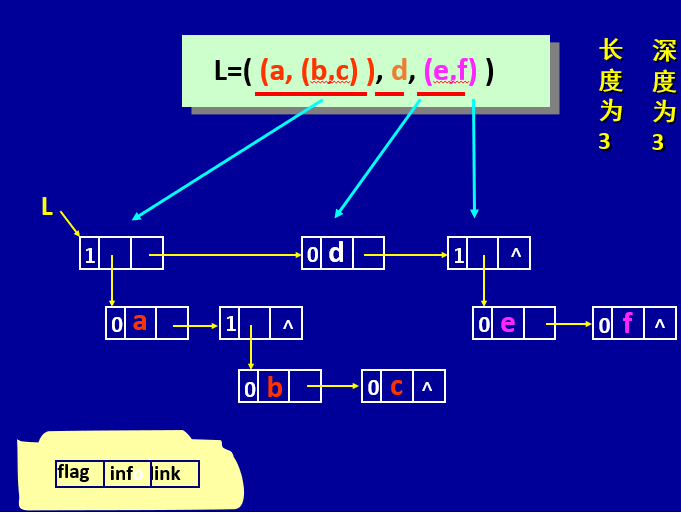
广义表的定义：一个长度为n≥0的广义表是一个数据结构。如LS = ( a1, a2, ……, an-1, an )。其中，LS为广义表的名字, ai为表中元素；ai可以是原子元素，也可以是一个子表。n为表的长度，长度为0的表称为空表。若ai为不可再分割的具体信息，则称ai 为原子元素；若ai 为一个子表，则称ai 为表元素。这里，用小写字母表示原子元素，用大写字母表示表元素。

广义表的例子

A = ();		// 长度为0的空表
B = (a);	// 长度为1，且只有一个原子元素的广义表
C = (a, (b, c));	// 长度为2的广义表
D = (A, B, c);		// 长度为3的广义表
E = (A, B, C);		// 长度为3的广义表
F = (a, F);			// 长度为2的递归的广义表

广义表的特点
1. 广义表是多层结构的
2. 广义表可为其他广义表所共享
3. 广义表可以是嵌套的
4. 广义表的深度——括号嵌套的重数

2.2 广义表的存储结构

链结点的构造

其中，flag为标志位, flag=0时表示本结点为原子结点，info域存放相应原子元素的信息；flag=1时表示本结点为表结点，info域存放子表第一个元素对应的链结点的地址。link域存放元素同一层的下一个元素所在链结点的地址，当本元素为所在层的最后一个元素时,link域为NULL。

类型定义

typedef struct node{
    int flag;
    union{
        DataType data;
        struct node *pointer;
    }info;
    struct node *link;
}BSNode, *BSLinkList;

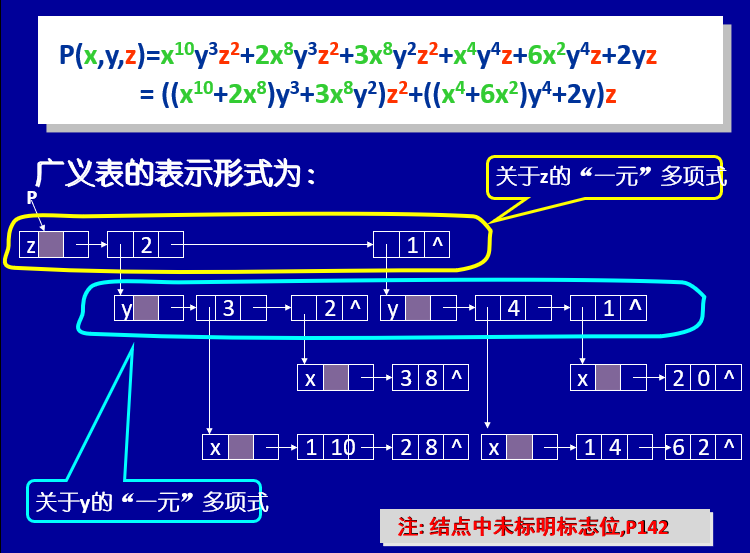
2.3 例：多元多项式的广义表表示

3 串

3.1 串的基本概念

串是由n>=0个字符组成的有限序列，记为S='a1 a2 a3 … an-1 an'其中, S表示串名（也称串变量）,一对引号括起来的字符序列称为串值,ai可以是字母、数字或其他允许的字符。n为串的长度，长度为0的串称为空串。
串值须用一对引号括起来，但引号不属于串值。

3.2 串的基本操作

3.3 串的存储结构

顺式存储结构
链式存储结构

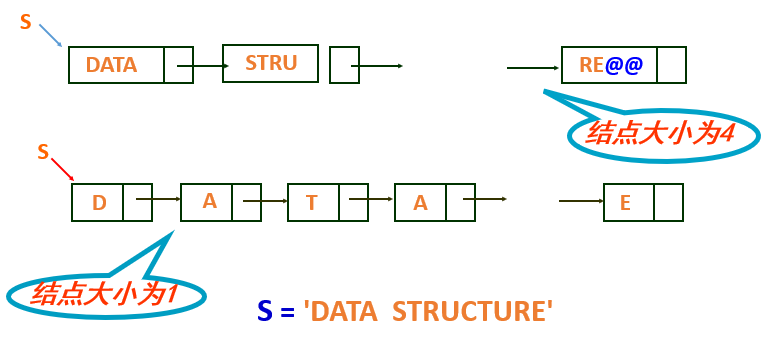
所谓链结点大小是指每个链结点的数据域中存放字符的个数。

3.4 关于串的几个算法

3.4.1 判断两个字符串是否相等

int equal(char s1[ ],char s2[ ]) {    
    int i=0;
    for(i=0; s1[i]!='\0' &&  s2[i]!='\0'; i++)
    	if(s1[i]!=s2[i])  
    		return  0;        /* 两个串不相等 */
    if(s1[i]=='\0' && s2[i]=='\0')  
    	return 1;               /* 两个串相等 */
    return 0;
}

3.4.2 串的插入

功能：在字符串s的第n个字符后面插入字符串t
前提：字符串s与t分别采用数组形式存储
约定：当n=0时，将t插在s的最前面；结果串由s指出
名词解释：
- 子串：串中若干个连续的字符组成的子序列。
- 主串：包含子串的串
- 位置：
  - 单个字符在主串中的位置被定义为该字符在串中的序号。
  - 子串在主串中的位置被定义为主串中首次出现的该子串的第一个字符在主串中的位置

// 代码实现1
int insert(char s[ ], char t[ ], int n){
    strcat(t, s+n);
    s[n] = '\0';
    strcat(s, t);
    return n;
}

// 代码实现2
int insert(char s[ ],char t[ ], int n) {    
    int i=0;
    char *p;
    p = (char *)malloc(strlen(s)+1);
    for(i=0; s[i+n] != '\0'; i++)
    	p[i] = s[i+n];
    for(i=n,j=0; t[j] != '\0'; i++,j++)
    	s[i] = t[j];
    for(j=0; p[j] != '\0'; i++,j++)
    	s[i] = p[j];
    free(p);
    return n;
}

3.4.3 串的模式匹配(Pattern Matching)

功能：字符串的定位。给定一个主字符串S和一个子串T(又称模式串)，长度分别为n和m。在主串S中，从起始位置开始查找，若在主串S中找到一个与子串T相等的子串，则返回T的第一个字符在主串中的位置序号。
串的简单模式匹配算法Brute-Force（布鲁特-福斯，又称朴素的模式匹配算法）算法：
- 将主串S的第一个字符和模式串T的第1个字符比较。若相等，继续逐个比较后续字符；若不等，从主串S的下一字符起，重新与T第一个字符比较。
直到主串S的一个连续子串字符序列与模式T相等。返回值为S中与T匹配的子序列第一个字符的序号，即匹配成功。否则，匹配失败，返回值 –1。

// 代码实现1
int index(char s[ ], char t[ ]){
    int i, j, k;
    for(i =0; s[i] != ‘\0’; i++){
        for(j=i, k=0; t[k]!=‘\0’ && s[j]==t[k]; j++, k++)
        	;
        if(t[k] == '\0')
        	return(i);
    }
    return ( -1);
}

// 代码实现2
int index(char S[ ], char T[ ]) {
    int i=0, j=0;
    while (S[i]!='\0' && T[j]!='\0') {
        if (S[i] == T[j]){
            i++;   
            j++ 
        }else{
            i = i-j +1;	
            j = 0; 		
        }
    }
    if(T[j] == '\0') 	
    	return i-j;  
    else    
    	return -1;                   
}

// 代码实现改进版
int index(char s[ ], char t[ ]){
    int i, j, k, n, m;
    n = strlen(s); 
    m = strlen(t);
    for(i =0; n-i >= m; i++){	// 当s中剩余字符数小于t中字符数时停止查找
        for(j=i,k=0;t[k]!=‘\0’&&s[j]==t[k]; j++,k++)
        	;
        if(t[k] == '\0')
        	return ( i);
    }
    return ( -1);
}

3.5 例：实现一个简化的Linux命令grep

3.5.1 问题提出

Linux系统中grep命令是一种强大的文本搜索工具，它能使用正则表达式搜索文本，并把匹配的行打印出来。grep全称是Global Regular Expression Print。其格式为：% grep [-acinv] [--color=auto] '搜寻字符串' filename。实现一个简化版的grep命令，其格式为：# grep [-i] [-n] [-v] '搜寻字符串' filename

选项与参数：

-i ：忽略大小写的不同，所以大小写视为相同

-n ：顺便输出行号

-v ：反向选择，亦即显示出没有 '搜寻字符串' 内容的那一行！

不支持正则表达式搜索
例如：将文件/etc/passwd中有root出现的行取出来,同时显示这些行在/etc/passwd中的行号

输入：# grep -n root /etc/passwd

输出：

1:root:x:0:0:root:/root:/bin/bash

30:operator:x:11:0:operator:/root:/sbin/nologin

3.5.2 算法设计

该问题的算法关键是在一个字符串（行）中查找另一个字符串。设：int index(char s[], char t[], int status)。返回0表示没有找到；返回非0正整数时，表示模式匹配成功次数。当status为0时表示严格匹配；为1时表示大小写无关匹配。

3.5.3 代码实现

朴素的Brute-Force算法

// 由于缺少46行的print函数，代码无法运行，但主要函数都写出来了
#include <stdio.h>
#include <ctype.h>
#include <string.h>
#include <math.h>
#include <stdlib.h>
#define MAXLEN 1024
int issame(char a, char b, int s);
int index(char s[ ], char t[ ], int status );

int main(int argc, char *argv[ ]){
    char line[MAXLEN], *pattern, *filename;
    int ai=0, an=0, av=0, lnum = 0, pos; //对应参数-i,-n,-v
    FILE *fp;
    if(argc<3 || argc>6){
        printf("usage: grep [-i] [-n] [-v] pattern filename\n");
    }else{
        pattern = argv[argc-2];
        filename = argv[argc-1];
        for( ; argc>3 ; argc--) {
            if(argv[argc-3][0] != '-') {
                printf("usage:grep  [-i] [-n] [-v] pattern filename\n");
            }else{
                switch (argv[argc - 3][1]) {
                    case 'i':
                        ai = 1;
                        break;
                    case 'n':
                        an = 1;
                        break;
                    case 'v':
                        av = 1;
                        break;
                    default:
                        printf("usage:  grep [-i] [-n] [-v] pattern filename\n");
                }
            }
        }
    }
    if((fp = fopen(filename, "r")) == NULL) {
        printf("Can open file\n");
    }else{
        while(fgets(line, MAXLEN-1, fp) !=NULL){
            lnum++;
            pos =  index(line, pattern, ai);
            print(line,lnum,pos,an,av);
        }
    }
    return 0;
}

int index(char s[ ], char t[ ], int status ){ //status为0：大小写敏感；status为1大小写无关
    int i, j, k,n,m,count=0;
    n = strlen(s);
    m = strlen(t);
    for(i =0; n-i >= m; i++){
        for(j=i,k=0; t[k]!='\0' && issame(s[j], t[k], status); j++,k++)
        ;
        if(t[k] == '\0')
        count++; //找到后，次数加1，继续查找
    }
    return  count;
}

int issame(char a, char b, int s){
    return s?(tolower(a) == tolower(b)) : (a == b);
}

KMP算法

（不要求自己写，会用就行）（效率比strstr没有很明显的提高，除非明摆着卡时长，否则没必要KMP）

KMP算法理解：KMP算法最浅显理解——一看就明白-CSDN博客

#include <stdio.h>
#include <ctype.h>
#include <string.h>
#include <math.h>
#include <stdlib.h>
#define MAXLINE 1024

void getnext(char T[], int next[]);
int KMPindex(char S[ ], char T[ ]);

int main( ){
    char filename[64], t[81], line[MAXLINE],*s;
    FILE *fp;
    int n,pos=0;
    scanf("%s %s", filename,t);
    if((fp = fopen(filename, "r")) == NULL){
        printf("Can't open file %s!\n", filename);
        return 1;
    }
    while(fgets(line, MAXLINE-1, fp) != NULL){
        s = line;
        while((n=KMPindex(s, t)) >= 0){     // 在s字符串查找t
            pos += n;
            printf("%d\n", pos);
            s = s+(n+1);
            pos++;
        }
    }
    return 0;
}

void getnext(char T[], int next[]){
    int i=0, j=-1;
    next[0]=-1;
    while(T[i]!='\0'){
        if(j==-1 || T[i]==T[j]){ //i为后缀位置；j为前缀位置
            i++;
            j++;
            next[i]=j;
        }else{
            j = next[j]; //若字符不同，则j值回溯
        }
    }
}

int KMPindex(char S[ ], char T[ ]){
    int i=0, j=0, *next;
    next = (int *)malloc(sizeof(int)*(strlen(T)+1));
    getnext(T, next);   // 获得next[t]
    while(S[i]!='\0' && T[j]!='\0'){
        if(S[i] == T[j]){
            i++;
            j++;
        }else{
            (j == 0) ? i++ :( j = next[j]); 		//j回退到相应位置开始匹配，i值不变
        }
    }
    free(next);
    if (T[j] == '\0') 	//匹配成功，返回匹配位置
        return i-j;
    else
        return -1;
}

学习经验 > 数据结构

#学习经验

【数据结构】ds笔记3-广义表、矩阵与串

http://example.com/2024/04/02/LE-ds3/

Author

John Doe

Posted on

April 2, 2024

Licensed under

【数据结构】ds笔记4-栈和队 Previous

【数据结构】ds笔记2-线性表 Next