【数据结构】ds笔记2-线性表

说在前面

本篇笔记总结了DSPv2b_2(线性表) for student内的相关内容，依旧将ppt分为两个部分————知识点和例题。以及注意本次学习内容为线性表，而非链表，并不是作业中的所有题目都需要用链表来完成，也记得利用好数组喵。以及如果你还想进行一些训练——洛谷欢迎您(https://www.luogu.com.cn/training/141312#problems)。最后，本人学艺不精，只是一边看着ppt一边敲敲改改，如有疏漏，欢迎提出喵~o( =∩ω∩= )m

知识点

1 外部（全局）变量

1.1 简介

外部变量（全局变量, global variable）：在函数外面定义的变量
作用于（scope）为整个程序，即可在程序的所有函数中使用
有隐含初值0
生存期（life cycle）：外部变量（存储空间）在程序执行过程中始终存在。

1.2 外部变量说明（extern）

C程序可以分别放在几个文件上，每个文件可作为一个编译单位分别编译。外部变量只需在某个文件上定义一次，其它文件若要引用此变量时，应用extern加以说明。（外部变量定义时不必加extern关键字）
1
2
3
4
5
6
7
8
9
10
11
12
13
14
// 第一个文件 int N; main(){ … N = … … } // 第二个文件 extern int N; fun(){ … N = … … }
在同一文件中，若前面的函数要引用后面定义的外部（在函数之外）变量时，也应在函数前加以extern说明。
1
2
3
4
5
6
7
8
9
10
extern int N; main(){ … N = … … } int N=0; void fun(){ … }

1.3 外部变量特点

使用外部变量的原因
1. 解决函数单独编译的协调；
2. 与变量初始化有关；
3. 外部变量的值是永久的；
4. 解决数据共享；
外部变量的副作用

使用外部变量的函数独立性差，通常不能单独使用在其他的程序中。而且，如果多个函数都使用到某个外部变量，一旦出现差错，就很难发现问题是由哪个函数引起的。在程序中的某个部分引起外部变量的错误，很容易误以为是由另一部分引起的。
建议：少用或不用外部变量

2 线性表

2.1 线性表的基本操作

创建一个新的线性表
求线性表的长度
检索线性表中的第i个数据元素
根据数据元素的某数据项(通常称为关键字)的值求该数据元素在线性表中的位置（查找）。
在线性表的第i个位置上存入一个新的数据元素。
在线性表的第i个位置上插入一个新的数据元素。
删除线性表中第i个数据元素。
对线性表中的数据元素按照某一个数据项的值的大小做升序或者降序排序。
销毁一个线性表
复制一个线性表
按照一定的原则，将两个或两个以上的线性表合并成为一个线性表。
按照一定的原则，将一个线性表分解为两个或两个以上的线性表

2.2 线性表的顺序存储结构

地址连续

基本操作

查找：确定元素item在长度为n的顺序表list中的位置

顺序查找、二分查找

插入：在长度为n的顺序表list的第i个位置上插入一个新的数据元素item

// 假设N是顺序表的长度（元素个数），为全局变量
int insertElem(ElemType list[], int i, ElemType item){
    int k;
    if(N==MaxSize || i<0 || i>N){	// 插入失败
        return -1;
    }
    for(k=N-1; k>=i; k--){		// 元素依次后移一个位置
        list[k+1] = list[k];
    }
    list[i] = item;
    N++;
    return 1;
}

删除：删除长度为n的顺序表list的某个数据元素

// 假设N是顺序表的长度（元素个数），为全局变量
int deleteElem(ElemType list[], int i){
    int k;
    if(N==0 || i<0 || i>N-1){		// 删除失败
        return -1;
    }
    for(k=i+1; k<N; k++){		// 元素依次前移一个位置
        list[k-1] = list[k];
    }
    N--;
    return 1
}

特点
1. 优点
  1. 构造原理简单、直观
  2. 读取速度快
  3. 存储空间开销小
  4. 查找效率高
2. 缺点
  1. 存储分配需要事先进行
  2. 需要一块地址连续的存储空间
  3. 基本操作（如插入、删除）的时间效率较低

2.3 线性表的链式存储结构

2.3.1 构造原理

用一组地址任意的存储单元(连续的或不连续的)依次存储表中各个数据元素, 数据元素之间的逻辑关系通过指针间接地反映出来。

2.3.2 线性链表的定义

链表定义

struct node {   
    ElemType data;
    struct node *next;
};
struct node *list, *p;

类型定义

struct node {   
    ElemType data;
    struct node *next;
};
typedef struct node *Nodeptr;
typedef struct node Node; 
Nodeptr list, p;

2.3.3 线性链表的基本操作

建立一个线性链表

Nodeptr createList(int n)  /*创建一个具有n个结点的链表 */
{
/* list是链表头指针, q指向新申请的结点，p指向最后一个结点*/
    Nodeptr  p, q, list=NULL;
    int i;
    for(i=0;i<n;i++){
        q=(Nodeptr)malloc(sizeof(Node));
        q->data=read();     	/* 取一个数据元素 */ 
        q->next=NULL;
        if (list==NULL) 	/*链表为空*/
            list=p=q;
        else
            p->next=q;       /* 将新结点链接在链表尾部 */
        p=q;
    }
    return list;
}

求线性链表的长度

// 非循环链表
int getLength(Nodeptr list){
    Nodeptr p;     // p为遍历链表结点的指针
    int n=0;                  // 链表的长度置初值0
    for(p=list; p!=NULL; p=p->next)		// p依次指向链表的下一结点
    	n++;    	　　// 对链表结点累计计数
    return n;                   // 返回链表的长度n
}
// 循环链表
int getlength( Nodeptr list ){
    Nodeptr p=list;
    int n=0;                        // 链表的长度置初值0
    if(list == NULL) return 0; 
    do{
        p=p->link;
        n++;
    }while(p!=list);
    return n;                       // 返回链表的长度n
}

输出一个表

void printList(List L) {
    while (L != NULL) {
        printf("%d ", L->data);
        L = L->next;
    }
}

删除

注意事项
1. 特殊情况：链表为空；删除头结点
2. 在删除某个结点时，必须要知道该结点的前序结点指针，否则无法删除。
3. 删除操作（函数）应返回头结点指针，如使用如下方式调用deleteNode删除函数，以保确头结点指向正确的结点：list = deleteNode(list, item);
4. 结点删除后一定要释放。删除某个结点前，必须要事先保存指向该结点的指针，以便删除后能释放结点。

删除p的下一个节点q（已知p的时候）

Nodeptr deleteNodepnext(Nodeptr list, Nodeptr p,  Nodeptr q){
    if(q==list)  
    	list=q->next;		/* 删除链表的第一个链结点*/
    else
    	p->next=q->next;	/* 删除p指的链结点*/
    free(q);				/* 释放被删除的结点空间*/
    return list；
}

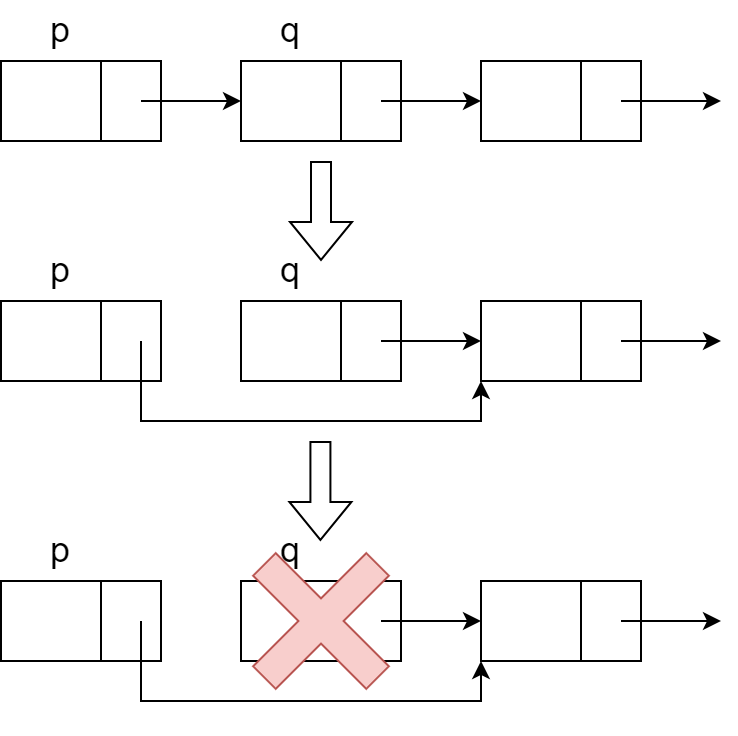
图片来源：https://onlyar.site/img/C-LinkedList.assets/delete.png

删除p结点

Nodeptr deleteNodep( Nodeptr list, Nodeptr p )
{
    Nodeptr r;
    if(p==list){                         // 当删除链表第一个结点
        list=list->next;
        free(p);                        // 释放被删除结点的空间
    }else{
        for(r=list; r->next!=p  &&  r->next!=NULL; r=r->next) 
        ;                           // 移向下一个链结点
        if(r->next!=NULL){ 		// r->next == p
            r->next=p->next;
            free(p);                  
        }
    } 
    return list;
}

删除包含给定元素的结点

Nodeptr deleteNode( Nodeptr list, ElemType elem ){
    Nodeptr p, q;    // p指向要删除的结点，q为p的前一个结点
	while(p->next != NULL){
        for(p=list; p!=NULL; q=p,p=p->next) 
            if(p->data==elem)         // 找到要删除的链结点
                break;
        if(p==list){                         // 删除头结点
            list = list->next;
            free(p);                  
        } 
        if(q->next != NULL){            // 删除p指向的结点
            q->next = p->next;
            free(p);
        }
    }
    return list;
 }

插入

注意事项：
1. 特殊情况：链表为空；在头节点前插入
2. 在某结点前插入一个结点，必须要知道该结点的前序结点指针，否则无法插入
3. 插入操作（函数）应返回头结点指针，如使用如下方式调用insertNode插入函数，以保确头结点指向正确的结点：list = insertNode(list, item);

在p后插入q

void insertNode(Nodeptr p, ElemType item){
    Nodeptr q;
    q = (Nodeptr) malloc (sizeof(Node));
    q->data = item;
    q->next = NULL;
    
    q->next = p->next;
    p->next = q;
}

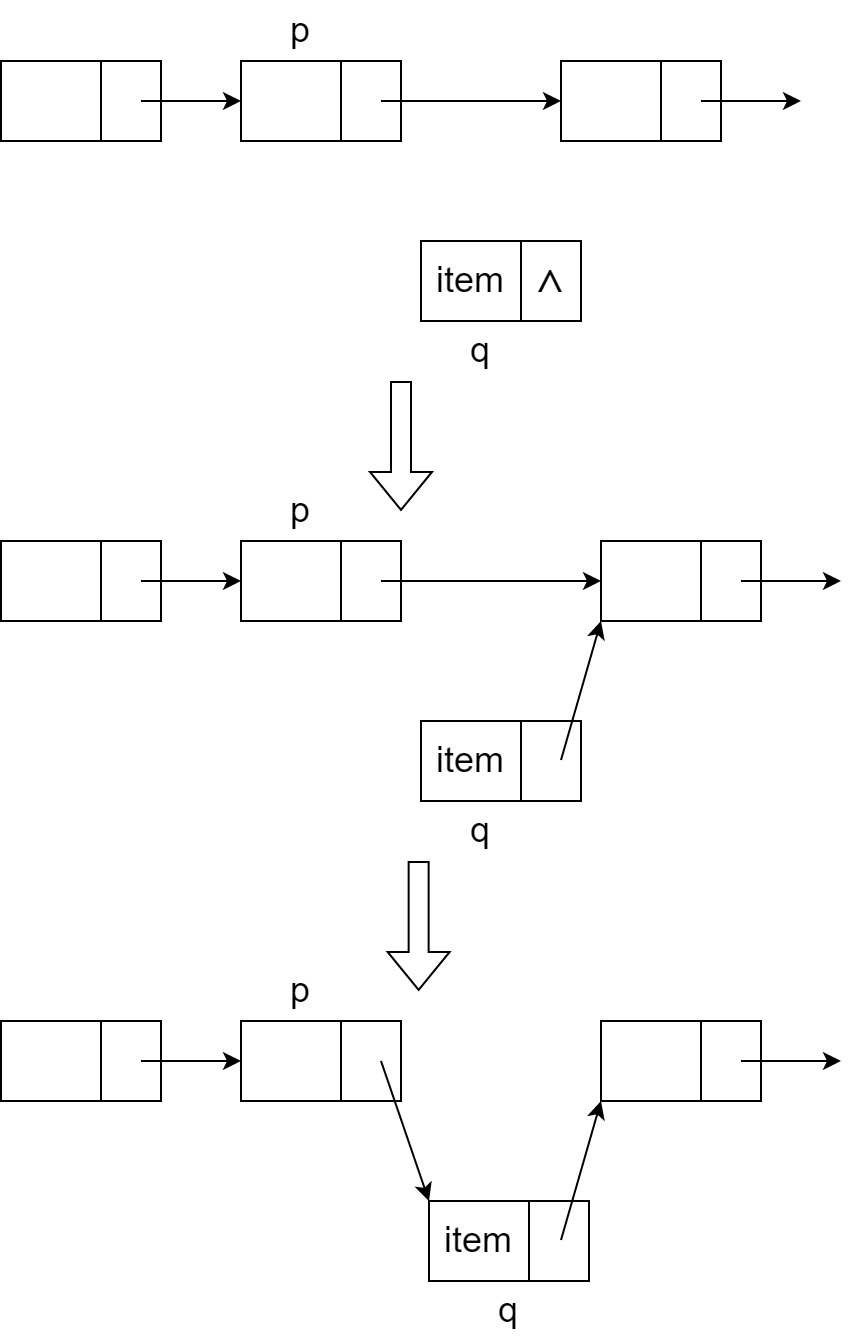
图片来源：https://onlyar.site/img/C-LinkedList.assets/insert.png

在链表头插入元素

Nodeptr insertFirst(Nodeptr list, ElemType item){
    // list指向链表的第一个结点
    p = (Nodeptr) malloc (sizeof(Node));
    p->data = item;		//将item赋给新结点数据域
    p->next = list;		//将新节点指向原链表第一个结点
    return p;	//返回新的链表表头指针
}
// 应使用如下方式调用insertFisrt函数：
// list = insertFirst(list, item);

在有序线性链表中相应位置上插入一个数据信息为item的链结点

/* 设list是一个有序增序链表，将元素elem插入到相应位置上 */
Nodeptr insertNode(Nodeptr list, ElemType elem){ 
    Nodeptr p,q, r;
    r = (Nodeptr)malloc(sizeof(Node)); //创建一个数据项为elem的新结点
    r->data = elem;
    r->next = NULL;
    
    if(list == NULL) 	 // list是一个空表
        return r;
    for(p=list; elem > p->elem && p != NULL;  q = p, p = p->next)
        // 找到插入位置
    ;
    
    if( p == list){ 	// 在头结点前插入
        r->link = p;
        return r;
    }else{ 				// 在结点q后插入一个结点
        q->next = r;
        r->next = p;
    }
    return list;
}
//调用方式
list = insertNode(list, item);

线性链表的逆转。
将两个线性链表合并为一个线性链表。
检索线性链表中的第i个链结点。
检索链表中数据信息
销毁一个表

又称哑结点dummy node，是在构造链表时会给链表设置一个标志结点。设置表头结点的最大好处是对链表结点的插入及删除操作统一了（不用考虑是否是头结点）。其数据域一般无意义（有时也可存放链表的长度）。

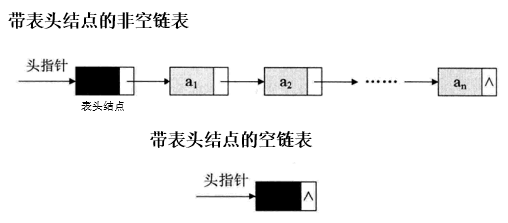
2.3.5 特点

优点
1. 存储空间动态分配，可以根据实际需要使用。
2. 不需要地址连续的存储空间(不需要大块连续空间)。
3. 插入/删除操作只须通过修改指针实现,不必移动数据元素，操作的时间效率高。（无论位于链表何处，无论链表的长度如何，插入和删除操作的时间都是O(1)。）
缺点
1. 每个链结点需要设置指针域(占用存储空间小)。
2. 是一种非连续存储结构，查找、定位等操作要通过顺序遍历链表实现，时间效率较低。（时间为O(n)）

2.4 顺序存储结构和链式存储结构的比较

1.若线性表需要频繁查找（通讯录），较少进行插入和删除操作时，宜采用顺序存储结构。若需要频繁插入和删除时（如词频统计），宜采用链表结构。

2.当线性表中的元素个数变化较大或者根本不知道有多大时（如词频统计单词表），最好用链表结构。而如果事先知道线性的大致长度，用顺序结构次效率会高些。

2.5 双向链表及其操作

2.5.1 双向链表的构造

双向链表指链表的每一个结点中除了数据域以外设置两个指针域，其中之一指向结点的直接后继结点，另外一个指向结点的直接前驱结点。
双向链表的几种形式

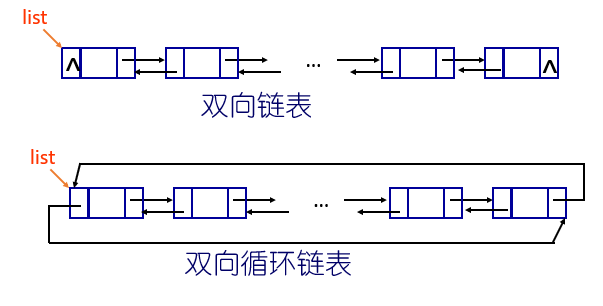
类型定义

struct node { 
    ElemType data;
    struct node *rlink, *llink;
};
typedef struct node *DNodeptr;
typedef struct node DNode;

2.5.2 双向链表的基础操作

双向链表的构建（构造有n个结点的双向链表）

DNodeptr initDLink(int n){
    int i;
    DNodeptr list,p;
    list=(DNodeptr) malloc (sizeof(DNode));
    READ(list->data);
    list->llink=list;
    list->rlink=list;
    for(i=1;i<n;i++){
        p=(DNodeptr) malloc (sizeof(DNode));
        READ(p->data);            /* 读入一元素 */
        insertNode(list,p);
    }
    return list;
}

双向链表的插入

插入到头结点左边

void insertNode(DNodeptr list, Dnodeptr p){
    list->llink->rlink=p;
    p->llink=list->llink;
    p->rlink=list;
    list->llink=p;
}

某个数据域的内容为x的链结点右边插入一个数据信息为item的新结点

原理

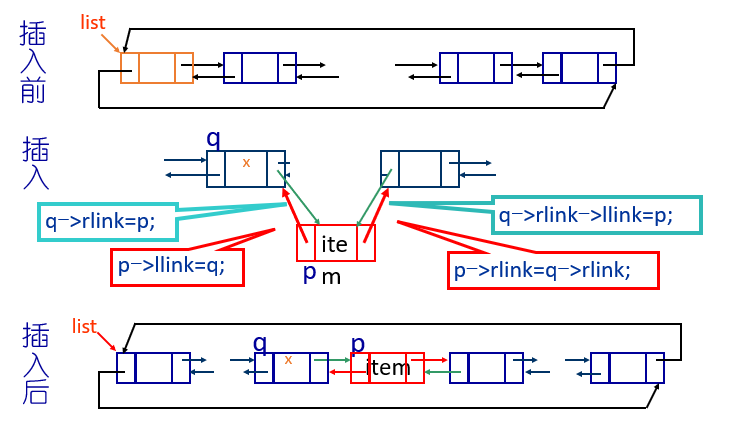
算法

int insertDNode(DNodeptr list, ElemType x, ElemType item){
    DNodeptr p, q;
    for(q=list; q->rlink!=list && q->data!=x; q=q->rlink);	// 寻找满足条件的链结点
    if(q->rlink == list && q->data != x){	// 没有找到满足条件的结点
        return -1;
    }
    p = (DNodeptr) malloc (sizeof(DNode));	// 申请一个新的结点
    p->data = item;
    p->llink = q;
    p->rlink = q->rlink;
    p->rlink->llink = p;
    q->rlink = p;
}

双向链表的删除

原理

算法

int deletDNode(DNodeptr list, ElemType x){
    DNodeptr q;
    for(q=list; q->rlink!=list && q->data!=x; q=q->rlink);		// 找满足条件的链结点
    if(q->rlink==list && q->data!=x){		// 没找到满足条件的结点
        return -1;
    }
    q->llink->rlink = q->rlink;
    q->rlink->llink = q->llink;
    free(q);
    return 1;
}

例题

例1 线性表的顺序存储结构

题目

已知长度为n 的非空线性表list采用顺序存储结构,并且数据元素按值的大小非递减排列(有序)，写一算法,在该线性表中插入一个数据元素item,使得线性表仍然保持按值非递减排列。

分析

1.寻找插入位置：从表的第一个元素开始进行比较，若有 item<a_i 则找到插入位置为表的第i个位置。

2.将第i个元素至第n个元素依次后移一个位置

3.将item插入表的第i个位置

4.表的长度增1。

代码实现

#include <stdio.h>
#define MAXSIZE 1000
typedef  int  ElemType;
int N=0; 
int main(){
    int i;
    ElemType  data,list[MAXSIZE];
    scanf("%d", &N);
    for(i=0; i<N; i++)
        scanf("%d", &list[i]);
    scanf("%d", &data);
    if(insertElem(list, data ) == 1)
        printf("OK\n");
    else 
        printf("Fail\n");
    return 0;
}

int insertElem(ElemType list[ ],  ElemType item){
    int i=0,j;
    if(N == MAXSIZE)
    	return -1; 
    i = searchElem(list, item);          /* 寻找item的合适位置 */
    for(j=N-1; j>=i; j--)
    	list[j+1]=list[j];
    list[i]=item;                       /* 将item插入表中 */
    N++;
    return 1;
}

int searchElem(ElemType list[ ], ElemType item){
    int low=0, high=n-1, mid;
    while(low <= high){
    	mid = (high + low) / 2;
        if( item < list[mid])
        	high = mid – 1;
        else if ( item > list[mid])
            low = mid + 1;
        else
            return (mid);
    }
    return low ;
}

例2 线性表的顺序存储结构

题目

编写程序统计一个文件中每个单词的出现次数（词频统计），并按字典序输出每个单词及出现次数。

分析

首先构造一个空的有序（字典序）单词表；
每次从文件中读入一个单词；
在单词表中（折半）查找该单词，若找到，则单词次数加1，否则将该单词插入到单词表中相应位置，并设置出现次数为1；
重复步骤2，直到文件结束。

代码实现

#include <stdio.h>
#include <string.h>
#include <ctype.h>
#define MAXWORD  32
#define MAXSIZE  1024
struct lnode {
    char word[MAXWORD];
    int count;
};

int getWord(FILE *bfp,char *w);
int searchWord(struct lnode list[], char *w);
int insertWord(struct lnode list[ ],  int pos, char *w);
int N=0; //单词表中单词的实际个数

int main(){
    struct lnode wordlist[MAXSIZE];	/*单词表*/
    int i;	
    char filename[MAXWORD], word[MAXWORD];
    FILE *bfp;

    scanf("%s", filename);
    if((bfp = fopen(bname, "r")) == NULL){		// 文件打开失败
        fprintf(stderr, "%s  can’t open!\n",filename);
        return -1;
     }
    while(getWord(bfp,word) != EOF)
        if(searchWord(wordlist, word) == -1) {	// 单词表满了
            fprintf(stderr, "Wordlist is full!\n");
            return -1;
        }
    for(i=0; i<= N-1; i++)
        printf("%s  %d\n", wordlist[i].word, wordlist[i].count);
    return 0;
}

例3 线性表的链式存储

题目

编写程序统计一个文件中每个单词的出现次数（词频统计），并按字典序输出每个单词及出现次数。

分析

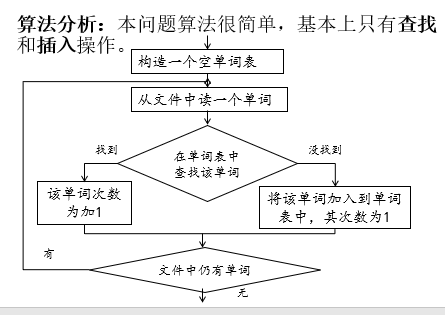
代码实现

// 我的代码
#include <stdio.h>
#include <ctype.h>
#include <string.h>
#include <math.h>
#include <stdlib.h>

struct list{
    char s[100];
    int sum;
};
struct list lists[100000];
int find(char s[], int ListNum);
int cmp(const void *pa, const void *pb);

int main() {
    FILE *in;       // 为读写文件定义文件指针
    in = fopen("article.txt", "r");      // 为输入打开一个给定文件"input.txt"；打开方式"r"为以只读方式打开一个文件
    char c='\0', s[100]={};
    int num=0, ListNum=0;   // num是单词有几个字母 ListNum是有几个单词
    while(fscanf(in, "%c", &c) != EOF){    //
        if(!isalpha(c)){        // 空格，句号，换行
            if(s[0]!='\0'){
                s[num]='\0';
                if(!find(s, ListNum)){       // 没出现过本单词
                    strcpy(lists[ListNum].s, s);
                    lists[ListNum].sum = 1;
                    ListNum++;
                }
            }
            // 初始化
            num = 0;
            strcpy(s, "\0");
            continue;
        }else{
            s[num] = tolower(c);
            num++;
        }
    }

    qsort(lists, ListNum, sizeof(struct list), cmp);
    for(int i=0; i<ListNum; i++){
        printf("%s %d\n", lists[i].s, lists[i].sum);
    }

    return 0;
}

int find(char s[], int ListNum){
    for(int i=0; i<ListNum; i++){
        if(strcmp(lists[i].s, s) == 0){
            lists[i].sum++;
            return 1;
        }
    }
    return 0;
}

int cmp(const void *pa, const void *pb){
    struct list *da = (struct list *)pa;
    struct list *db = (struct list *)pb;
    if(strcmp(da->s, db->s) < 0){
        return -1;
    }else{
        return 1;
    }
}

// ppt的代码
#include <stdio.h>
#include <string.h>
#inlcude <stdlib.h>
#define MAXWORD  32
struct node {
    char word[MAXWORD];
    int count;
    struct node *link;
} ; //单词表结构
struct node *Wordlist = NULL; //单词表头指针
int getWord(FILE *bfp,char *w);
int searchWord(char *w);
int insertWord( struct node *p, char *w);

int main(){
    char filename[32], word[MAXWORD];
    FILE *bfp;
    struct node *p;

    scanf(“%s”, filename);
    if((bfp = fopen(filename, “r”)) == NULL){ //打开一个文件
        fprintf(stderr, “%s  can’t open!\n”,filename);
        return -1;
    }
    while(getWord(bfp,word) != EOF) //从文件中读入一个单词
        if(searchWord(word) == -1) { //在单词表中查找插入单词
            fprintf(stderr, “Memory is full!\n”);
            return -1;
        }
    for(p=Wordlist; p != NULL; p=p->link) //遍历输出单词表
    	printf(“%s  %d\n”, p->word, p->count);
    return 0;
} 

/*在链表中p结点后插入包含给定单词的结点，同时置次数为1*/
int insertWord(struct node  *p, char *w){
    struct node  *q;

    q = (struct node * )malloc(sizeof(struct node));
    if(q == NULL) return -1; //没有内存空间
    strcpy(q->word, w);
    q->count = 1;
    q->link = NULL;              
    if(Wordlist == NULL){ //空链表
    	Wordlist = q;
    }else if(p == NULL){ //插入到头结点前
        q->link = Wordlist;
        Wordlist = q;
    }else{
        q->link = p->link;
        p->link = q;
    }
    return 0;
}

/*在链表中查找一单词，若找到，则次数加1；否则将该单词插入到有序表中相应位置，同时次数置1*/
int searchWord(char *w){
    struct  node *p, *q=NULL; //q为p的前序结点指针
    for(p=Wordlist; p != NULL; q=p,p=p->link){
        if(strcmp(w, p->word) < 0){ 
        	break;
        }else if(strcmp(w, p->word) == 0){
            p->count++;
            return 0 ;
        }
    }
    return insertWord(q, w);
}

例4 单向链表、链表的合并

题目

【问题描述】编写一个程序实现任意（最高指数为任意正整数）两个一元多项式相加。
【输入形式】从标准输入中读入两行以空格分隔的整数，每一行代表一个多项式，且该多项式中各项的系数均为0或正整数。对于多项式a_nxⁿ + a_n-1x^n-1+ … + a₁x¹ + a₀x⁰的输入方法如下：a_n n a_n-1 n-1 … a₁ 1 a₀ 0，即相邻两个整数分别表示表达式中一项的系数和指数。在输入中只出现系数不为0的项。
【输出形式】将运算结果输出到屏幕。将系数不为0的项按指数从高到低的顺序输出，每次输出其系数和指数，均以一个空格分隔。最后要求换行。
【样例输入】

54 8 2 6 7 3 25 1 78 0

43 7 4 2 8 1
【样例输出】

54 8 43 7 2 6 7 3 4 2 33 1 78 0
【样例说明】输入的两行分别代表如下表达式：

54x⁸ + 2x⁶ + 7x³ + 25x + 78

43x⁷ + 4x² + 8x

其和为 54x⁸ + 43x⁷ + 2x⁶ + 7x³ + 4x² + 33x + 78

分析

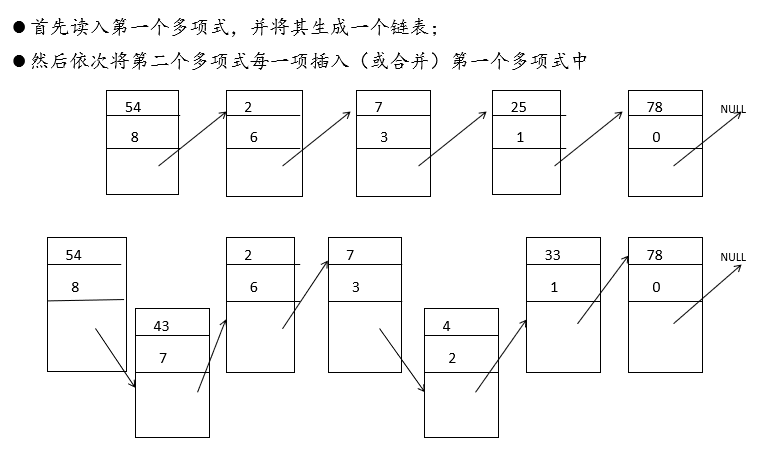
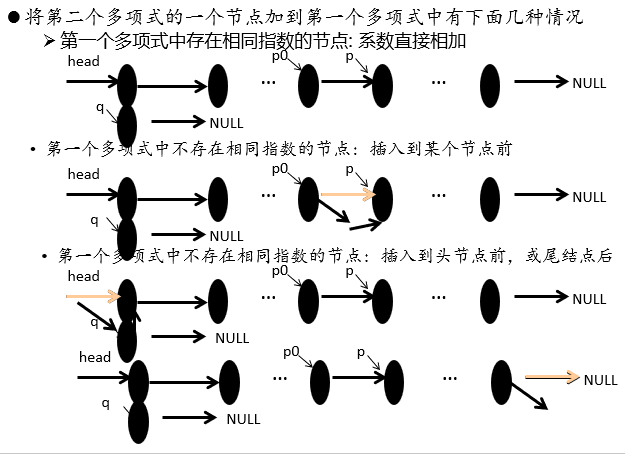
代码实现

//c3_4c.c
#include <stdio.h>
#include <stdlib.h>
struct  Node { //一个多项式节点结构
    int coe; //系数
    int pow; //幂
    struct Node *next;
}; 
int main(){
    int a,n;
    char c;
    struct Node *head,*p,*q,*p0;
    head = p = NULL;
    do {  //创建一个链表存放第一个多项式
        scanf(“%d%d%c”, &a, &n, &c);
        q =  (struct Node *)malloc(sizeof(struct Node));
        q->coe = a; q->pow = n; q->next = NULL;
        if(head == NULL){
             head = p = q;
		}else{
            p->next = q;
            p = p->next;
    	}
    } while ( c != ‘\n’);
    do { //将第二个多项式的每个项插入到第一个多项式链表中
        scanf(“%d%d%c”, &a, &n, &c);//生成第二个多项式的一个节点
        q = (struct Node *)malloc(sizeof(struct Node));
        q->coe = a; q->pow = n; q->next = NULL;
        for(p=head; p!=NULL; p0=p,p=p->next) {
            if(q->pow > p->pow) { 
				if(p==head) { q->next = head; head = q; break; }//插入到头节点前
				else { q->next = p; p0->next = q; break;} //将q插入到p前
            }
            else if(q->pow == p->pow)  { p->coe += q->coe; break;}//指数相等，系数相加
         }
         if(p== NULL)  p0->next = q;   //将q插入到尾节点后
    } while ( c != ‘\n’);
    for(p=head; p!=NULL; p=p->next)		//输出
		printf(“%d  %d  “, p->coe,p->pow);
    return 0;
}

例5 循环链表

题目

已知n个人（不妨分别以编号1,2,3,…,n代表）围坐在一张圆桌周围，编号为k的人从1开始报数,数到m的那个人出列，他的下一个人又从1开始继续报数,数到m的那个人出列,…,依此重复下去，直到圆桌周围的人全部出列。

代码实现

#include <stdio.h>
#include <ctype.h>
#include <string.h>
#include <math.h>
#include <stdlib.h>

struct link {
    int i;
    struct link *next;
};

int main() {
    int n, m;
    scanf("%d%d", &n, &m);
    struct link *first=NULL, *p,*q;
    for(int i=1; i<=n; i++){
        q = (struct link *)malloc(sizeof(struct link));		// 创建一个新的节点（本节点）
        q->i = i;
        q->next = NULL;
        if(first == NULL){		// 第一个节点
            first = p = q;
        }else{
            p->next = q;	// 使前一个节点指向本节点（当前的最后一个节点）
            p = p->next;	// 指针p继续移动，指向当前的最后一个节点
        }
    }
    q->next = first;
    struct link *flag = first;
    for(int j=0; j<n; j++){
        for(int i=1; i<m; i++){
            if( i!=m-1 ){
                flag = flag->next;
            }else{
                p = flag->next; //第3个
                printf("%d ", p->i);    //第3个
                flag->next = flag->next->next;  // 第二个的下一个是第四个
                free(p);
                flag = flag->next;
            }
        }
    }

    return 0;
}

例6 循环链表

题目

问题：命令tail用来显示一个文件的最后n行。其格式为：tail [-n] filename其中：n表示需要显示的行数，省略时n的值为10；filename为给定文件名。如，命令tail –20 example.txt表示显示文件example.txt的最后20行。实现该程序，该程序应具有一定的错误处理能力，如能处理非法命令参数和非法文件名。

分析

如何得到需要显示的行数和文件名？
- 使用命令行参数int main(int argc, char *argv[])
- 行数n = atoi(argv[1]+1)
- 文件名filename = argv[2]
如何得到最后n行？

使用n个节点的循环链表。链表中始终存放最近读入的n行。首先创建一个空的循环链表；然后再依次读入文件的每一行挂在链表上，最后链表上即为最后n行

代码实现

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define DEFLINES  10
#define MAXLEN    81
struct Node {
    char *line;
    struct Node *next;
};
int main(int argc, char *argv[ ])
{
    char curline[MAXLEN],*filename;
    int n = DEFLINES, i;
    struct Node *first, *ptr;
    FILE *fp;
    if( argc == 3 && argv[1][0] == '-') {	// 命令行输入中指定打印行数时，获取行数及文件名。如tail -20 test.txt
		n = atoi(argv[1]+1);
        filename = argv[2];
    }
    else if( argc == 2){		
        // 命令行输入中没有指定打印行数时，获取文件名，此时行数为缺省10。如tail  test.txt
        filename = argv[1];
    }else{
		printf("Usage: tail [-n] filename\n");
        return (1);
	}
	if((fp = fopen(filename, "r")) == NULL){	// 创建循环链表
		printf(" Cann't open file: %s !\n", filename);
		return (-1);
	}
    first = ptr = (struct Node *)malloc(sizeof ( struct Node));
    first->line = NULL;
    for(i=1; i<n; i++){
        ptr->next = (struct Node *)malloc(sizeof ( struct Node));
        ptr = ptr->next;
        ptr->line = NULL;
    }
    ptr->next = first;
    ptr = first;	// 将链表的最后一个节点指向头节点，以构成一个循环链表。
    
	while(fgets(curline, MAXLEN, fp) != NULL){
        if(ptr->line != NULL)        /*链表已经满了，需要释放掉不需要的行*/
			free(ptr->line);
        ptr->line = (char *) malloc ( strlen(curline)+1);
        strcpy(ptr->line, curline);
        ptr = ptr->next;
	}
    for(i=0; i<n; i++) {
        if(ptr->line != NULL)
        	printf("%s",ptr->line);
        ptr = ptr->next;
    }
    fclose(fp);
    return 0;
}

学习经验 > 数据结构

#学习经验

【数据结构】ds笔记2-线性表

http://example.com/2024/03/23/LE-ds2/

Author

John Doe

Posted on

March 23, 2024

Licensed under

【数据结构】ds笔记3-广义表、矩阵与串 Previous

【学习经验】exe bat 和 PATH Next

【数据结构】ds笔记2-线性表

说在前面

知识点

1 外部（全局）变量

1.1 简介

1.2 外部变量说明（extern）

1.3 外部变量特点

2 线性表

2.1 线性表的基本操作

2.2 线性表的顺序存储结构

2.3 线性表的链式存储结构

2.3.1 构造原理

2.3.2 线性链表的定义

2.3.3 线性链表的基本操作

2.3.4 表头结点(header)

2.3.5 特点

2.4 顺序存储结构和链式存储结构的比较

2.5 双向链表及其操作

2.5.1 双向链表的构造

2.5.2 双向链表的基础操作

例题

例1 线性表的顺序存储结构

题目

分析

代码实现

例2 线性表的顺序存储结构

题目

分析

代码实现

例3 线性表的链式存储

题目

分析

代码实现

例4 单向链表、链表的合并

题目

分析

代码实现

例5 循环链表

题目

代码实现

例6 循环链表

题目

分析

代码实现